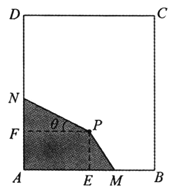
题目内容
【题目】设有三点
，其中点
在椭圆
上，
，
，且
.
（1）求椭圆
的方程；
（2）若过椭圆的右焦点的直线
倾斜角为
，直线与椭圆相交于
，求三角形
的面积.
【答案】（1）
； （2）
.
【解析】
（1）先求得
的值.设出
点坐标，代入
，化简后可求得点坐标，将点坐标代入椭圆方程，由此求得
的值，并求出椭圆方程.（2）由（1）求得椭圆焦点的坐标，利用点斜式得到直线
的方程，联立直线的方程和椭圆的方程，利用两点间距离公式求得
的长度，利用点到直线的距离公式求得
到直线的距离，由此求得三角形
的面积.
（1）解：由题意知，
，
设
，
，
，
由，∴
，
∴
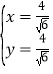
设椭圆方程
②，将①代入②，
∴
，
∴椭圆方程为
（2）
，
∴
的方程
代入，整理得
，
∴
或
，
∴交点坐标为
和
，到的距离为
所以
，
所以三角形的面积为.
练习册系列答案
阅读快车系列答案
相关题目
