题目内容
已知A﹑B﹑C是直线上的三点,向量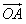 ﹑
﹑ ﹑
﹑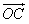 满足
满足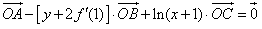 ;
;
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0, 证明:f(x)>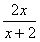 ;
;
(Ⅲ)当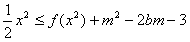 时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围。
时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围。
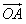 ﹑
﹑ ﹑
﹑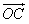 满足
满足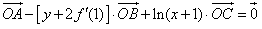 ;
;(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0, 证明:f(x)>
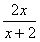 ;
;(Ⅲ)当
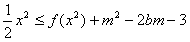 时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围。
时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围。 解:(Ⅰ)由三点共线知识,
∵ ,
,
∴ ,
,
∵A﹑B﹑C三点共线,
∴ ,
,
∴ ,
,
∴ ,
, ,
,
∴f(x)=ln(x+1)。
(Ⅱ)令g(x)=f(x)- ,
,
由 ,
,
∵x>0,
∴ ,
,
∴g(x)在 (0,+∞)上是增函数,
故g(x)>g(0)=0,即f(x)> 。
。
(Ⅲ)原不等式等价于 ,
,
令h(x)= =
= ,
,
由
当x∈[-1,1]时,[h(x)]max=0,
∴m2-2bm-3≥0,
令Q(b)= m2-2bm-3,
则由Q(1)≥0及Q(-1)≥0,解得m≤-3或m≥3。
∵
 ,
,∴
 ,
,∵A﹑B﹑C三点共线,
∴
 ,
,∴
 ,
,∴
 ,
, ,
,∴f(x)=ln(x+1)。
(Ⅱ)令g(x)=f(x)-
 ,
,由
 ,
,∵x>0,
∴
 ,
,∴g(x)在 (0,+∞)上是增函数,
故g(x)>g(0)=0,即f(x)>
 。
。(Ⅲ)原不等式等价于
 ,
,令h(x)=
 =
= ,
,由

当x∈[-1,1]时,[h(x)]max=0,
∴m2-2bm-3≥0,
令Q(b)= m2-2bm-3,
则由Q(1)≥0及Q(-1)≥0,解得m≤-3或m≥3。

练习册系列答案
相关题目
 ,那么b与c夹角是
,那么b与c夹角是
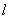 上的三点,向量
上的三点,向量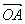 ﹑
﹑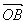 ﹑
﹑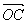 满足:
满足:
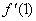 ]·
]·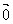 ;
; ;
;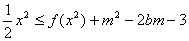 时,x
时,x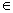
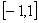 及b
及b