题目内容
如图所示,等腰△ABC的底边AB=6 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记 ,用
,用 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.

(Ⅰ)求
 的表达式;
的表达式;
(Ⅱ)当x为何值时, 取得最大值?
取得最大值?
(Ⅲ)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
【答案】
(Ⅰ)
 (Ⅱ)
(Ⅱ) 时
时 取得最大值(Ⅲ)
取得最大值(Ⅲ)
【解析】
试题分析:(Ⅰ)根据四棱锥的体积公式可知 ,
,
即
 ;
;
(Ⅱ) ,
,
 时,
时,
 时,
时,
 时
时 取得最大值.
取得最大值.
(Ⅲ)以E为空间坐标原点,直线EF为 轴,直线EB为
轴,直线EB为 轴,直线EP为
轴,直线EP为 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 ;
;
 ,
,
设异面直线AC与PF夹角是 ,
,
 .
.
考点:本小题主要考查四棱锥的体积,异面直线所成的角,函数的最值.
点评:本小题融合了四棱锥的体积计算,函数的最值,异面直线所成的角等问题,比较综合,但是难度不大,求解时要注意取值范围.

练习册系列答案
相关题目
 短长度为
短长度为 如图所示,等腰△ABC的底边AB=6
如图所示,等腰△ABC的底边AB=6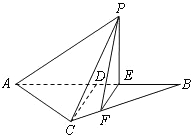 如图所示,等腰△ABC的底边
如图所示,等腰△ABC的底边 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记 ,用
,用 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.