题目内容
20.已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,且焦距为4.(1)求椭圆的方程;
(2)直线l过点P(0,2)且与椭圆相交于A、B两点,当△AOB面积取得最大值时,求直线l的方程.
分析 (1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).由条件得b=c=2,a2=b2+c2=8,解出即可;
(2)直线l的斜率一定存在,设直线l的方程为:y=kx+2(k≠0),联立直线和椭圆方程,消去y得关于x的方程,运用弦长公式以及三角形的面积公式,再由基本不等式即可得到最大值.
解答 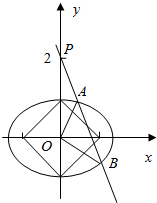 解:(1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
解:(1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
则由条件得,b=c=2,a2=b2+c2=8
故椭圆方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1;
(2)直线l的斜率一定存在,设直线l的方程为:y=kx+2(k≠0),
由y=kx+2和椭圆方程$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1,联立,消去y得
(1+2k2)x2+8kx=0,
设A(x1,y1),B(x2,y2),则x1,=0,x2=-$\frac{8k}{1+2{k}^{2}}$,
∴|AB|=$\sqrt{1+{k}^{2}}$•|$\frac{8k}{1+2{k}^{2}}$|,
又O到直线AB的距离为d=$\frac{2}{\sqrt{{k}^{2}+1}}$,
∴S△AOB=$\frac{1}{2}$|AB|d=|$\frac{8k}{1+2{k}^{2}}$|=$\frac{8}{\frac{1}{|k|}+2|k|}$≤$\frac{8}{2\sqrt{2}}$=2$\sqrt{2}$
当且仅当k=$\frac{\sqrt{2}}{2}$时,取等号,
此时直线方程为y=±$\frac{\sqrt{2}}{2}$x+2.
点评 本题考查椭圆的方程和性质及运用,考查直线和椭圆方程联立,消去一个未知数,运用韦达定理,和弦长公式,考查运算求解能力,属于中档题.

| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
| A. | [-$\frac{1}{6}$,$\frac{5}{3}$] | B. | (-∞,-$\frac{1}{6}$]∪[$\frac{5}{3}$,+∞) | C. | [-$\frac{1}{6}$,0)∁(0,$\frac{5}{3}$] | D. | (-$\frac{1}{6}$,$\frac{5}{3}$) |
| A. | {-4,-3,0,2,3} | B. | {-3,-2,0,1,3} | C. | {-3,-1,0,1,2} | D. | {-4,-3,0,1,2} |
| A. | $\frac{9}{4}$ | B. | 4 | C. | $\frac{9}{4}$或4 | D. | $\frac{3}{2}$ |