题目内容
定义在 上的偶函数
上的偶函数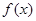 满足
满足 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则
是钝角三角形的两个锐角,则 与
与 的大小关系是
的大小关系是
A. | B. |
C. | D. |
B
解析试题分析:由 得,
得,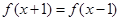 ,函数的对称轴是
,函数的对称轴是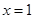 。因为函数
。因为函数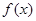 为偶函数,且在
为偶函数,且在 上是减函数,所以函数在
上是减函数,所以函数在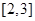 上是增函数。结合对称轴知,函数在
上是增函数。结合对称轴知,函数在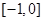 上是减函数,则在
上是减函数,则在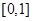 上是增函数。由于
上是增函数。由于 是钝角三角形的两个锐角,所以
是钝角三角形的两个锐角,所以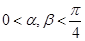 ,即有
,即有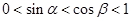 ,所以
,所以 。故选B。
。故选B。
考点:函数的单调性
点评:本题关键是确定函数在区间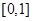 的单调性。另在确定单调性过程中,假如两个区间关于对称轴对称,则函数在这两个区间中的单调性相反。
的单调性。另在确定单调性过程中,假如两个区间关于对称轴对称,则函数在这两个区间中的单调性相反。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
函数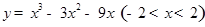 有 ( )
有 ( )
A.最大值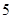 ,最小值-22 ,最小值-22 | B.最大值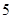 ,最小值-2 ,最小值-2 |
C.最大值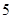 ,无最小值 ,无最小值 | D.最小值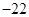 ,无最大值 ,无最大值 |
若函数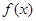 为奇函数,且当
为奇函数,且当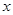 >0时
>0时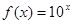 ,则
,则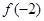 的值是( )
的值是( )
A.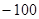 | B.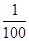  | C.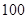 | D.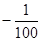 |
已知函数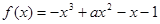 在
在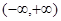 上是单调函数,则实数
上是单调函数,则实数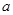 的取值范围是( )
的取值范围是( )
A.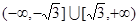 | B.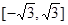 |
C.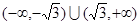 | D.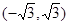 |
已知函数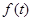 是奇函数且是
是奇函数且是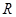 上的增函数,若
上的增函数,若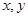 满足不等式
满足不等式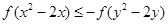 ,则
,则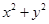 的最大值是( )
的最大值是( )
A. | B.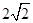 | C.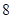 | D.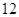 |
已知偶函数 满足当x>0时,
满足当x>0时, ,则
,则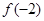 等于
等于
A.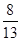 | B. | C.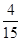 | D. |
对于R上可导的任意函数f(x),若满足(x-1)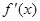 ³ 0,则必有 ( )
³ 0,则必有 ( )
| A.f(0)+ f(2)< 2 f(1) | B.f(0)+ f(2)£ 2 f(1) |
| C.f(0)+ f(2)³ 2 f(1) | D.f(0)+ f(2)> 2 f(1) |
下列整数中,小于-3的整数是
| A.-4 | B.-2 | C.0 | D.3 |
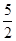 )= ( )
)= ( )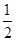 B.-
B.-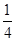 C .
C .