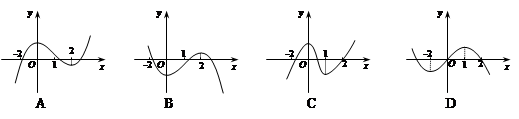题目内容
已知函数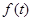 是奇函数且是
是奇函数且是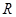 上的增函数,若
上的增函数,若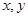 满足不等式
满足不等式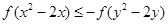 ,则
,则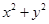 的最大值是( )
的最大值是( )
A. | B.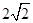 | C.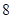 | D.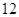 |
C
解析试题分析:解:∵f(x2-2x)≤-f(y2-2y),,∴f(x2-2x)≤f(-y2+2y),,∵f(x)是增函数,∴x2-2x≤-y2+2y,整理得(x-1)2+(y-1)2≤2,设点P的坐标为(x,y)则点P是以(1,1)为圆心,, 为半径的圆上及以内的点,而此圆过原点,则
为半径的圆上及以内的点,而此圆过原点,则 为点P到原点的距离,∵圆过原点,∴
为点P到原点的距离,∵圆过原点,∴ 的最大值为圆的直径2
的最大值为圆的直径2 ∴x2+y2的最大值为8故选C
∴x2+y2的最大值为8故选C
考点:函数的奇偶性,不等式
点评:本题主要考查了函数的奇偶性的应用及解不等式的问题.解题的关键是根据不等式的形式利用数形结合的方法直观的解决问题

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
设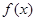 为定义在
为定义在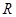 上的奇函数,当
上的奇函数,当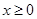 时,
时,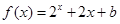 (
( 为常数),则
为常数),则
| A.-3 | B.-1 | C.1 | D.3 |
函数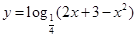 的单调递增区间是( )
的单调递增区间是( )
A.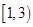 | B.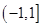 | C.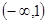 | D. |
若定义在 上的函数
上的函数 满足:对任意
满足:对任意 ,有
,有 ,则下列说法一定正确的是( )
,则下列说法一定正确的是( )
A. 为奇函数 为奇函数 | B. 为偶函数 为偶函数 |
C. 为奇函数 为奇函数 | D. 为偶函数 为偶函数 |
定义在 上的偶函数
上的偶函数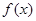 满足
满足 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则
是钝角三角形的两个锐角,则 与
与 的大小关系是
的大小关系是
A. | B. |
C. | D. |
若函数 的零点与
的零点与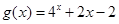 的零点之差的绝对值不超过
的零点之差的绝对值不超过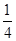 ,则
,则 可以是
可以是
A. =4x-1 =4x-1 | B. =(x-1)2 =(x-1)2 |
C. =ex-2 =ex-2 | D.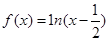 |
下列函数中,在 内为增函数的是( )
内为增函数的是( )
A. | B. |
C. | D. |
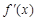 的图象如图所示,那么函数f (x)的图象最有可能的是( )
的图象如图所示,那么函数f (x)的图象最有可能的是( )