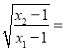Question

【题目】已知函数f(x)=lnx-a．

(1)若a=-1，求曲线y=f(x)在点(1,f(1))处的切线方程；

(2)若f(x)恒成立，求实数a的取值范围．

Answer 1

【答案】(1) x-y-2=0 (2)

【解析】

（1）利用曲线的切线方程公式，求得结果;

（2）由题，进行变形为f(x)恒成立，即f(x)恒成立，构造新函数，用参变分离求函数单调性求其最值，求得a的范围.

函数f(x)的定义域为(0,+)

（1）a=-1时，f(x)=lnx-．,,

，且f(1)=-1.

所以曲线在点(1,f(1))处的切线方程为y-(-1)=x-1，

即x-y-2=0.

（2）若f(x)恒成立，即f(x)恒成立．

设g(x)=f(x)-x=lnx--a，只要即可；

．

①当a=0时，令，得x=1.

x,变化情况如下表：

x	(0,1)	1	(1,+)
	+	0	-
g(x)	↗	极大值	↘

所以，故满足题意.

②当a时，令，得x=-（舍）或x=1；

x,变化情况如下表：

x	(0,1)	1	(1,+)
	+	0	-
g(x)	↗	极大值	↘

所以，令，得.

③当时，存在x=2-

满足g(2-)=ln(2-)，

所以f(x)不能恒成立，所以不满足题意.

综上，实数a的取值范围为.