Question

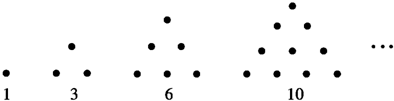
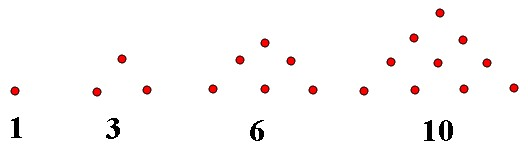
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数. 他们研究过如图所示的三角形数：

将三角形数1，3，6，10，记为数列，将可被5整除的三角形数按从小到大的顺序组成一个新数列. 可以推测：

（Ⅰ）是数列中的第         项；

（Ⅱ）________（用k表示）

 

Answer 1

【答案】

（Ⅰ）9；（Ⅱ）

【解析】

试题分析：（I）由题设条件可以归纳出，故，由此可知，第3个可被5整除的数为45，是数列中的第9项；

（II）由于是偶数，由（I）知，第个被5整除的数出现在第组倒数第一个，故它是数列中的第项，所以.

考点：本小题主要考查数列的递推关系，数列的表示及归纳推理，考查学生的归纳推理能力.

点评：解决此小题的关键是由题设得出相邻两个三角形数的递推关系，由此列举出三角形数.