题目内容
16.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,直线l:y=$\frac{1}{2}$x交椭圆于A、B两点,点F关于直线l的对称点E恰好在椭圆上,且|AE|+|BF|=6,则椭圆的短轴长为4.分析 设F(c,0),左焦点为F',运用垂直平分线的性质和椭圆的定义可得a=3,设E(m,n),由对称可得$\frac{n-0}{m-c}$=-2,$\frac{1}{2}$n=$\frac{m+c}{4}$,求出E的坐标,代入椭圆方程,化简整理,计算即可得到所求值.
解答  解:设F(c,0),左焦点为F',由垂直平分线的性质可得|AE|=|AF|,
解:设F(c,0),左焦点为F',由垂直平分线的性质可得|AE|=|AF|,
又|BF|=|AF'|,
由|AE|+|BF|=6,可得|AF|+|AF'|=2a=6,即a=3,
设E(m,n),由对称可得$\frac{n-0}{m-c}$=-2,$\frac{1}{2}$n=$\frac{m+c}{4}$,
解得m=$\frac{3}{5}$c,n=$\frac{4}{5}$c,
代入椭圆方程可得$\frac{9{c}^{2}}{25×9}$+$\frac{16{c}^{2}}{25{b}^{2}}$=1,
由c2=9-b2,化简可得b4+32b2-144=0,
解得b=2,
可得椭圆的短轴长为4. 故答案为:4.
点评 本题考查椭圆的短轴长的求法,注意运用椭圆的定义和点关于直线的对称的结论,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
4.已知A,B分别为椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当$\frac{2b}{a}+\frac{a}{b}+\frac{1}{2mn}$+ln|m|+ln|n|取最小值时,椭圆C的离心率为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
8.已知函数f(x)=ln$\frac{x}{2}$+$\frac{1}{2}$,g(x)=ex-2,若g(m)=f(n)成立,则n-m的最小值为( )
| A. | 1-ln2 | B. | ln2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
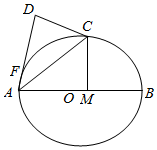 如图,AB是圆O的直径,C,F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C,且交AF的延长线于点D,CM⊥AB,垂足为点M.
如图,AB是圆O的直径,C,F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C,且交AF的延长线于点D,CM⊥AB,垂足为点M.