题目内容
(14分)已知函数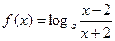 的定义域为[
的定义域为[ ,
, ],值域为
],值域为 ,
,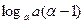 ],并且
],并且 在
在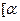 ,
,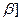 上为减函数.
上为减函数.
(1)求 的取值范围;
的取值范围;
(2)求证: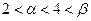 ;
;
(3)若函数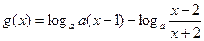 ,
,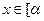 ,
,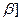 的最大值为M,
的最大值为M,
求证: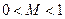
解.(1)按题意,得 .
.
∴  即
即  . 3分
. 3分
又 ∴ 关于x的方程
∴ 关于x的方程 .
.
在(2,+∞)内有二不等实根x=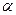 、
、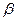 .
. 关于x的二次方程
关于x的二次方程
 在(2,+∞)内有二异根
在(2,+∞)内有二异根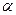 、
、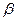 .
. . 故
. 故  . 6分
. 6分
(2)令 ,则
,则

 .
.
∴ 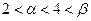 . 10分
. 10分
(3)∵  ,
,
 .
.
∵  , ∴ 当
, ∴ 当 (
(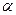 ,4)时,
,4)时, ;当
;当 (4,
(4,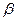 )是
)是 .
.
又 在[
在[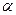 ,
,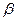 ]上连接, ∴
]上连接, ∴  在[
在[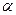 ,4]上递增,在[4,
,4]上递增,在[4,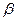 ]上递减.
]上递减.
故  . 12分
. 12分
∵  , ∴ 0<9a<1.故M>0. 若M≥1,则
, ∴ 0<9a<1.故M>0. 若M≥1,则 .
.
∴  ,矛盾.故0<M<1. 14分
,矛盾.故0<M<1. 14分
解析

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
在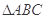 中,若
中,若 ,则
,则 与
与 的大小关系为( ).
的大小关系为( ).
A. | B. | C. | D. 、 、 的大小关系不能确定 的大小关系不能确定 |
函数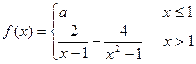 在x=1处连续,则
在x=1处连续,则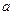 =
=
A. | B.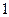 | C. | D.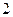 |
 设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
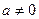 时,求:函数
时,求:函数 的单调区间;
的单调区间; 时,求证:当
时,求证:当 时,不等式
时,不等式
 x)能否由y=log3x的图象平移变换得到;
x)能否由y=log3x的图象平移变换得到;
 的图像在点
的图像在点 处
处 平行.
平行. 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
 在
在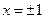 处取得极值。
处取得极值。 的解析式;
的解析式; Ⅱ)求证:对于区间
Ⅱ)求证:对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
; 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。
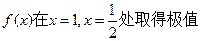 ,
, 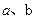 的值;
的值;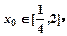 使得不等式
使得不等式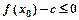 成立,求
成立,求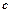 的最小值;
的最小值;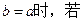
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。