题目内容
(本小题满分14分) 已知函数 在
在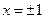 处取得极值。
处取得极值。
(Ⅰ)求函数 的解析式;
的解析式;
( Ⅱ)求证:对于区间
Ⅱ)求证:对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
;
(Ⅲ)若过点 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。
(Ⅰ)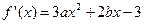 ,依题意,
,依题意,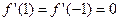 ,………1分
,………1分
即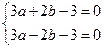 ,解得
,解得 …………………3分
…………………3分
经检验符合。
(Ⅱ)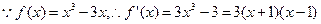
当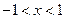 时,
时,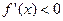 ,故
,故 在区间
在区间 上为减函数,
上为减函数,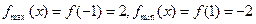 ……………………5分
……………………5分
∵对于区间 上任意两个自变量的值
上任意两个自变量的值 ,
,
都有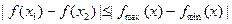
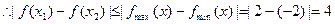 …………………………7分
…………………………7分
(Ⅲ)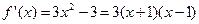 ,
,
∵ 曲线方程为
曲线方程为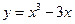 ,∴点
,∴点 不在曲线上,
不在曲线上,
设切点为M(x0,y0),则点M的坐标满足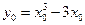 。
。
因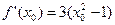 ,故切线的斜率为
,故切线的斜率为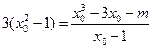 ,
,
整理得 。
。
∵过点A(1,m)可作曲线的三条切线,
∴关于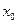 的方程
的方程 有三个实根。……………9分
有三个实根。……………9分
设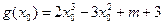 ,则
,则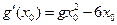 ,
,
解析

练习册系列答案
相关题目
函数y=sin(x+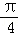 )的一个单调增区间是( ).
)的一个单调增区间是( ).
| A.[﹣π,0] | B.[0,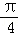 ] ] | C.[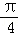 , ,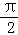 ] ] | D.[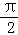 ,π] ,π] |
 时,f
时,f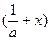 >f
>f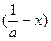 ;
;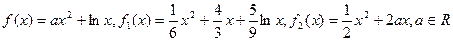 .
. 在点
在点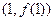 处的切线恒过定点,并求出定点坐标;
处的切线恒过定点,并求出定点坐标;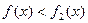 在区间
在区间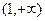 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;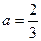 时,求证:在区间
时,求证:在区间 恒成立的函数
恒成立的函数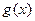
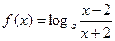 的定义域为[
的定义域为[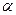 ,
,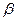 ],值域为
],值域为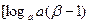 ,
,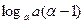 ],并且
],并且 在
在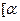 ,
,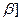 上为减函数.
上为减函数. 的取值范围;
的取值范围; 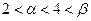 ;
;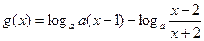 ,
,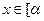 ,
,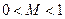
 ,其中
,其中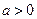 .
.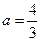 时,求
时,求 的极值点;
的极值点; 的取值范围.
的取值范围. .
. 中,若
中,若 ,
, (
( ),则
),则 .
.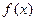 =
=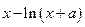 在
在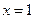 处取得极值.
处取得极值. 的值;
的值;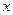 的方程
的方程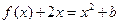 在
在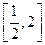 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数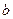 的取值范围;
的取值范围; .参考数据:
.参考数据: