题目内容
（09年湖北八校联考理）（13分）
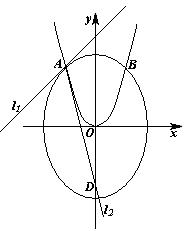
如图，已知曲线
与抛物线
的交点分别为
、
，曲线
和抛物线
在点处的切线分别为
、
，且、的斜率分别为
、
.
（Ⅰ）当
为定值时，求证
为定值（与
无关），并求出这个定值；
（Ⅱ）若直线与
轴的交点为
，当
取得最小值
时，求曲线和的方程。
解析：（Ⅰ）设点
的坐标为
，
曲线
的方程可写成：
，∴
∴
…2′
又
…………4′
∴
为定值。……6′
（Ⅱ）如图设点的坐标为
，则
.
由（Ⅰ）知：
，则直线
.
∵
过点
，则
，即
，∴点
.…8′
将代入曲线的方程得
.
∴
.
由重要不等式得
.……10′
当且仅当“
”成立时，有
，解得
∴
，
.……13′
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，函数
的图像在点
的切线方程是
．
的解析式：
上是单调函数，求实数
的取值范围．
的各棱长都为
，
为棱
上的动点．
时，求证：
． 
，求二面角
的大小． 
到平面
的距离． 
各棱长都为
，
为棱
上的动点。
的值，使得
；
，求二面角
的大小；
到面
的距离。
，
（
，
）.函数
，
的图象的一个对称中心与它相邻的一条对称轴之间的距离为
，且过点
.
的表达式；
时，求函数