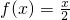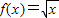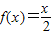Question

对任意正数的x₁，x₂，都有f（x₁•x₂）=f（x₁）+f（x₂）成立，且f（4）=2由此下列合适的函数是（　　）

• A、f(x)=

  x

• B、f（x）=log₂x
• C、f(x)=

  x

  2

• D、f（x）=2^x

Answer 1

分析：对任意正数的x₁，x₂，都有f（x₁•x₂）=f（x₁）+f（x₂）成立，且f（4）=2，由此关系对四个选项进行验证即可得到正确选项

解答：解：A不对，不满足对任意正数的x₁，x₂，都有f（x₁•x₂）=f（x₁）+f（x₂）成立；
B正确，符合题设中的条件；
C不正确，不满足对任意正数的x₁，x₂，都有f（x₁•x₂）=f（x₁）+f（x₂）成立；
D不正确，不满足对任意正数的x₁，x₂，都有f（x₁•x₂）=f（x₁）+f（x₂）成立，且f（4）=2
故选B

点评：本题考查对数的运算性质，求解本题的关键是理解题设中所给的函数的性质，然后用这些特征比对四个函数，得到正确选项．