题目内容
设抛物线x2=2py(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥y轴.证明直线AC经过原点O.
证:设AB:y=kx+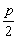 ,代入x2=2py,得x2-2pmx-P2=0.
,代入x2=2py,得x2-2pmx-P2=0.
由韦达定理,得xAxB=-p2,
即xB=-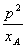 .
.
∵BC∥y轴,且C在准线y=-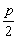 上,
上,
∴C(xB,-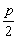 ).
).
则kOC=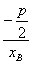 =
=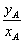 =kOA.
=kOA.
故直线AC经过原点O.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
设抛物线x2=2py(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥y轴.证明直线AC经过原点O.
证:设AB:y=kx+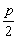 ,代入x2=2py,得x2-2pmx-P2=0.
,代入x2=2py,得x2-2pmx-P2=0.
由韦达定理,得xAxB=-p2,
即xB=-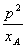 .
.
∵BC∥y轴,且C在准线y=-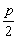 上,
上,
∴C(xB,-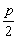 ).
).
则kOC=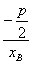 =
=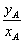 =kOA.
=kOA.
故直线AC经过原点O.

 阅读快车系列答案
阅读快车系列答案