题目内容
已知圆C1的方程为(x-2)2+(y-1)2=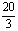 ,椭圆C2的方程为
,椭圆C2的方程为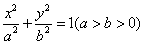 ,C2的离心率为
,C2的离心率为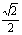 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
(I)直线AB的方程;
(II)椭圆C2的方程.
(I)由e=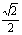 ,得
,得 =
= ,a2=2c2,b2=c2。 ...........2分
,a2=2c2,b2=c2。 ...........2分
设椭圆方程为 +
+ =1。又设A(x1,y1),B(x2,y2)。由圆心为(2,1),得x1+x2=4,y1+y2=2。
=1。又设A(x1,y1),B(x2,y2)。由圆心为(2,1),得x1+x2=4,y1+y2=2。
又 +
+ =1,
=1, +
+ =1,两式相减,得
=1,两式相减,得  +
+ =0。
=0。
∴ ...........5分
...........5分
∴直线AB的方程为y-1= -(x-2),即y= -x+3。 ...........6分
(II)将y= -x+3代入 +
+ =1,得3x2-12x+18-2b2=0
=1,得3x2-12x+18-2b2=0
又直线AB与椭圆C2相交,∴Δ=24b2-72>0。 ...........8分
由|AB|= |x1-x2|=
|x1-x2|=
 =
= ,
,
得 ·
· =
= 。
。
解得 b2=8, ...........11分
故所求椭圆方程为 +
+ =1 ...........12分
=1 ...........12分

练习册系列答案
相关题目
 ,则目标函数z=x+2y的最小值为________
,则目标函数z=x+2y的最小值为________  +
+ =1所表示的曲线为C,给出下列四个命题:
=1所表示的曲线为C,给出下列四个命题: ;
; .
. 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 B
B  D
D 
 ”的逆否命题为“若
”的逆否命题为“若
 ”
” ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 为假命题,则
为假命题,则 均为假命题
均为假命题 则
则 

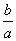 ,1},N={a,0},f:x→x表示把M中的元素x映射到集合N中仍为x,则a+b等于( )
,1},N={a,0},f:x→x表示把M中的元素x映射到集合N中仍为x,则a+b等于( )