题目内容

已知椭圆C:+=1(a＞b＞0).

(1)若点P(x0,y0)是椭圆C内部的一点，求证：+＜1;

(2)若椭圆C:+=1(a＞b＞0)上存在不同的两点关于直线l:y=x+1对称，试求a、b满足的关系式.

(1)证明：设F1、F2为椭圆C的左、右两个焦点.∵P是椭圆C内部的一点，

    ∴|F1P|+|F2P|＜2a.

    ∴+＜2a.

    ∴(a2-c2)x02+a2y02＜a2(a2-c2).

    ∴+＜1(b2=a2-c2).

(2)解：设椭圆C上关于直线l对称的点A、B的坐标为A(x1,y1)、B(x2,y2)，线段AB的中点坐标为M(xm,ym),则有

   

    ②-①得b2(x22-x12)+a2(y22-y12)=0,

    b2(x2-x1)(x2+x1)+a2(y2-y1)(y2+y1)=0,

    b2xm+a2ym=0,

    把③代入上式得b2xm-a2ym=0,    ⑤

    由④和⑤得xm=,ym=,

    即M(,).

    ∵点M在椭圆C的内部，

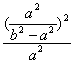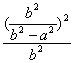    ∴+＜1.

    ∴a2+b2＜(b2-a2)2=(a+b)2(a-b)2.

    a、b应满足的不等式为a2+b2＜(a+b)2(a-b)2.


练习册系列答案
相关题目
已知椭圆C 1：
x2
a2
+
y2
b2
=λ1（a＞b＞0，λ1＞0）和双曲线C 2：
x2
m2
-
y2
n2
=λ2(λ2≠0)，给出下列命题：
①对于任意的正实数λ1，曲线C1都有相同的焦点；
②对于任意的正实数λ1，曲线C1都有相同的离心率；
③对于任意的非零实数λ2，曲线C2都有相同的渐近线；
④对于任意的非零实数λ2，曲线C2都有相同的离心率．
其中正确的为（　　）

（07年陕西卷） (14分)

已知椭圆C:=1(a＞b＞0)的离心率为,短轴一个端点到右焦点的距离为.

(Ⅰ)求椭圆C的方程;

(Ⅱ)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为，求△AOB面积的最大值.

已知椭圆C:=1()的离心率为,短轴一个端点到右焦点的距离为.

(1)求椭圆的方程；

(2)设直线与椭圆交于、两点，坐标原点到直线的距离为，求△面积的最大值.

已知椭圆C:+=1(a>b>0)的一个顶点为A(2,0),离心率为.直线y=k(x-1)与椭圆C交于不同的两点M,N.

(1)求椭圆C的方程;

(2)当△AMN的面积为时,求k的值.

 

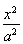
（本小题满分12分）

       已知椭圆C: +=1（a＞b＞0）的离心率e=，且椭圆经过点N（2，-3）．

   （1）求椭圆C的方程；

   （2）求椭圆以M（-1，2）为中点的弦所在直线的方程．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网