Question

已知椭圆C: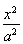+=1(a>b>0)的一个顶点为A(2,0),离心率为.直线y=k(x-1)与椭圆C交于不同的两点M,N.

(1)求椭圆C的方程;

(2)当△AMN的面积为时,求k的值.

 

Answer 1

【答案】

(1) +=1 (2) k=±1

【解析】

解:(1)由题设知,椭圆焦点在x轴上,

∴a=2.

由e==得c=,

∴b2=a2-c2=2.

∴椭圆C的方程为+=1.

(2)由消去y,

整理得(1+2k2)x2-4k2x+2k2-4=0.

设M(x1,y1),N(x2,y2).

则Δ=(-4k2)2-4(1+2k2)(2k2-4)>0(※)

且x1+x2=,x1·x2=,

∴|MN|=

=

=

=

=

设点A(2,0)到直线y=k(x-1)的距离为d,

则d=.

∴S△AMN=|MN|·d==,

解得k=±1,

代入(※)式成立,∴k=±1.