题目内容
过点P(2,1)的直线l交x轴、y轴正半轴于A、B两点,求使:
(1)△AOB面积最小时l的方程;
(2)|PA||PB|最小时l的方程.
(1)△AOB面积最小时l的方程;
(2)|PA||PB|最小时l的方程.
分析:设出直线的截距式方程,利用直线经过点(2,1),得到关系式,
(1)通过基本不等式求出ab的最小值,然后求解△AOB面积最小时l的方程;
(2)利用推出的关系式,通过距离公式化简|PA||PB|,利用基本不等式求出最小值时a,b的值,然后求出l的方程.
(1)通过基本不等式求出ab的最小值,然后求解△AOB面积最小时l的方程;
(2)利用推出的关系式,通过距离公式化简|PA||PB|,利用基本不等式求出最小值时a,b的值,然后求出l的方程.
解答:解:设直线的方程为
+
=1(a>2,b>1),
∵直线l过点P(2,1),
∴
+
=1.
(1)∵2
≤
+
=1,
∴ab≥8.∴S△AOB=
ab≥
×8=4.
当且仅当
=
=
,即a=4,b=2时,S△AOB取最小值4,
此时直线l的方程为
+
=1,即x+2y-4=0.
(2)由
+
=1,得ab-a-2b=0,
变形得(a-2)(b-1)=2,
|PA||PB|=
•
=
≥
.
当且仅当a-2=1,b-1=2,即a=3,b=3时,|PA|•|PB|取最小值4.
此时直线l的方程为x+y-3=0.
| x |
| a |
| y |
| b |
∵直线l过点P(2,1),
∴
| 2 |
| a |
| 1 |
| b |
(1)∵2
|
| 2 |
| a |
| 1 |
| b |
∴ab≥8.∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当
| 2 |
| a |
| 1 |
| b |
| 1 |
| 2 |
此时直线l的方程为
| x |
| 4 |
| y |
| 2 |
(2)由
| 2 |
| a |
| 1 |
| b |
变形得(a-2)(b-1)=2,
|PA||PB|=
| (2-a)2+(1-0)2 |
| (2-0)2+(1-b)2 |
| [(a-2)2+1]•[(b-1)2+4] |
| 2(a-2)•4(b-1) |
当且仅当a-2=1,b-1=2,即a=3,b=3时,|PA|•|PB|取最小值4.
此时直线l的方程为x+y-3=0.
点评:本题考查直线方程的应用,基本不等式求解最值问题,考查转化思想以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 椭圆E:
椭圆E: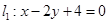 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
.