题目内容
甲、乙两人参加一次智力测试,在已知备选的10道题中,甲能答对其中的5道题,乙能答对其中8道题,规定每次测试都从备选题中随机抽出3道题进行测试,至少答对2题才算合格.
(1)求甲答对试题数X的概率分布及数学期望;
(2)求甲、乙两人至少有一人测试合格的概率.
解:(1)由题设知X可能取的值为0,1,2,3,
P(X=0)= =
= ,
,
P(X=1)= =
= ,
,
P(X=2)= =
= ,
,
P(X=3)= =
= ,
,
∴ =
= .
.
(2)设甲测试合格记为事件A,设乙测试合格记为事件B,
则P(A)= =
= ,
,
P(B)= =
=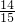 ,
,
∴甲、乙两人至少有一人测试合格的概率:
P=1-P( )P(
)P( )=1-(1-
)=1-(1- )(1-
)(1-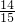 )=
)= .
.
分析:(1)由题设知X可能取的值为0,1,2,3,分别求出P(X=0),P(X=1),P(X=2),P(X=3),能求出EX.
(2)设甲测试合格记为事件A,设乙测试合格记为事件B,则P(A)= =
= ,P(B)=
,P(B)= =
=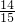 ,由P=1-P(
,由P=1-P( )P(
)P( ),能求出甲、乙两人至少有一人测试合格的概率.
),能求出甲、乙两人至少有一人测试合格的概率.
点评:本题考查离散型随机变量的数学期望,是历年高考的重点题型.解题时要认真审题,注意对立事件的概率的灵活运用.
P(X=0)=
 =
= ,
,P(X=1)=
 =
= ,
,P(X=2)=
 =
= ,
,P(X=3)=
 =
= ,
,∴
 =
= .
.(2)设甲测试合格记为事件A,设乙测试合格记为事件B,
则P(A)=
 =
= ,
,P(B)=
 =
=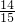 ,
,∴甲、乙两人至少有一人测试合格的概率:
P=1-P(
 )P(
)P( )=1-(1-
)=1-(1- )(1-
)(1-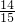 )=
)= .
.分析:(1)由题设知X可能取的值为0,1,2,3,分别求出P(X=0),P(X=1),P(X=2),P(X=3),能求出EX.
(2)设甲测试合格记为事件A,设乙测试合格记为事件B,则P(A)=
 =
= ,P(B)=
,P(B)= =
=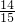 ,由P=1-P(
,由P=1-P( )P(
)P( ),能求出甲、乙两人至少有一人测试合格的概率.
),能求出甲、乙两人至少有一人测试合格的概率.点评:本题考查离散型随机变量的数学期望,是历年高考的重点题型.解题时要认真审题,注意对立事件的概率的灵活运用.

练习册系列答案
相关题目
 如图是一次考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是
如图是一次考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是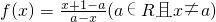 .
.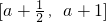 时,求证:f(x)的值域为[-3,-2];
时,求证:f(x)的值域为[-3,-2];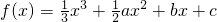 ,其中a,b,c∈R.
,其中a,b,c∈R.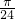



 表示双曲线,若P∨Q为假命题,求实数m的取值范围.
表示双曲线,若P∨Q为假命题,求实数m的取值范围. 如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若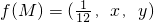 ,且ax+y-108xy≥0恒成立,则正实数a的最小值为________.
,且ax+y-108xy≥0恒成立,则正实数a的最小值为________.