题目内容

已知函数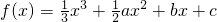 $数学公式$ ，其中a，b，c∈R．
（Ⅰ）若a=1，b=-2，求f（x）的单调递减区间；
（Ⅱ）若f（x）在区间[-1，1）、（1，3]内各有一个极值点，且f（-1）≤0恒成立，求c的取值范围；
（Ⅲ）对于给定的实数a、b、c，函数f（x）图象上两点A（x₁，f（x₁）），B（x₂，f（x₂））（x₁≠x₂）处的切线分别为l₁，l₂．若直线l₁与l₂平行，证明：A、B关于某定点对称，并求出该定点．

（Ⅰ）解：当a=1，b=-2时，f′（x）=x²+x-2＜0，解得-2＜x＜1，故递减区间为（-2，1）．
（Ⅱ）解：f′（x）=x²+ax+b，又f（x）区间[-1，1），（1，3]内各有一个极值点，
所以 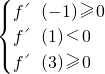$\text{[math]}$ ，即 $\text{[math]}$ ，
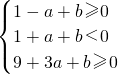其中点（a，b）是以A（0，-1），B（-2，-3），C（-4，3）为顶点的三角形内部的点，或线段BC（不含点C）、线段AB（不含点A）上的点．
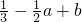又 $\text{[math]}$ ，即 $\text{[math]}$ 恒成立，即求 $\text{[math]}$ 的最小值，
由图可知 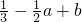$\text{[math]}$ 的最小值在B（-2，-3）点处取到，故 $\text{[math]}$ ，即 $\text{[math]}$ ．
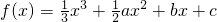（Ⅲ）证明：因为 $\text{[math]}$ ，所以f'（x）=x²+ax+b，
所以l₁，l₂的斜率分别为 $\text{[math]}$ ， $\text{[math]}$ ．
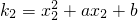又直线l₁与l₂平行，所以k₁=k₂，即 $\text{[math]}$ = $\text{[math]}$ ，
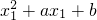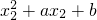因为x₁≠x₂，所以x₁+x₂=-a，从而x₂=-（a+x₁），
所以 $\text{[math]}$ = $\text{[math]}$ ．
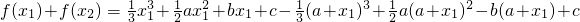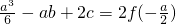又由上 x₁+x₂=-a，所以点A（x₁，f（x₁）），B（x₂，f（x₂））（x₁≠x₂）关于点 $\text{[math]}$ 对称．
故当直线l₁与l₂平行时，点A与点B关于点 $\text{[math]}$ 对称．
注：对称点也可写成 $\text{[math]}$
分析：（Ⅰ）求导函数，令f′（x）＜0，可得函数递减区间；
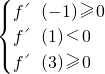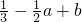（Ⅱ）求导函数，利用f（x）区间[-1，1），（1，3]内各有一个极值点，可得 $\text{[math]}$ ，根据f（-1）≤0恒成立，可得 $\text{[math]}$ 恒成立，求 $\text{[math]}$ 的最小值即可；
（Ⅲ）求导函数，利用直线l₁与l₂平行，可得斜率相等，从而可得x₁+x₂=-a，计算f（x₁）+f（x₂），即可得到结论．
点评：本题考查导数知识的运用，考查函数的单调性，考查恒成立问题，考查点的对称性，属于中档题．