题目内容

若双曲线 $数学公式$ 的离心率为 $数学公式$ ，则两条渐近线的方程为________．

$\text{[math]}$
分析：通过离心率，推出a，b的关系，即可求出两条渐近线的方程．
解答：双曲线 $\text{[math]}$ 的离心率为 $\text{[math]}$ ，
所以 $\text{[math]}$ ，又c²=a²+b²，
所以 $\text{[math]}$ ，
所以 $\text{[math]}$ ，
$\text{[math]}$ 的两条渐近线的方程为 $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题考查双曲线的渐近线方程的求法，注意双曲线的形式，考查计算能力．

练习册系列答案

100分闯关期末冲刺系列答案

绩优课堂单元达标创新测试卷系列答案

名校秘题冲刺卷系列答案

神龙牛皮卷期末100分闯关系列答案

状元成才路创新名卷系列答案

优优好卷单元测评卷系列答案

名校联盟快乐课堂系列答案

开心夺冠系列答案

同步测控全优设计系列答案

领航新课标练习册系列答案

相关题目

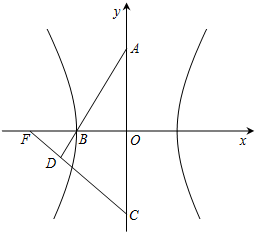如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为2，则∠BDF的余弦值是（　　）

若双曲线的离心率为2，两焦点坐标为（-2，0），（2，0），则此双曲线的方程为

（2013•天津）已知双曲线

=1(a＞0，b＞0)的两条渐近线与抛物线y²=2px（p＞0）的准线分别交于A，B两点，O为坐标原点．若双曲线的离心率为2，△AOB的面积为

，则p=（　　）

（2012•黄州区模拟）已知双曲线的顶点与焦点分别是椭圆

=1(a＞b＞0)的焦点与顶点，若双曲线的离心率为2，则椭圆离心率为（　　）

已知双曲线

=1（a＞0，b＞0）的两条渐近线与抛物线y²=2px（p＞0）的准线分别交于A，B两点，O为坐标原点．若双曲线的离心率为2，△AOB的面积为