题目内容
已知函数f(x)= ex,a,b
ex,a,b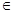 R,且a>0.
R,且a>0.
⑴若a=2,b=1,求函数f(x)的极值;
⑵设g(x)=a(x-1)ex-f(x).
①当a=1时,对任意x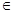 (0,+∞),都有g(x)≥1成立,求b的最大值;
(0,+∞),都有g(x)≥1成立,求b的最大值;
②设g′(x)为g(x)的导函数.若存在x>1,使g(x)+g′(x)=0成立,求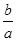 的取值范围.
的取值范围.
⑴f (x)的极大值是f (-1)=e-1,f (x)的极小值是f (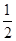 )=4
)=4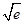 ;⑵① -1-e-1 ;②(-1,+∞).
;⑵① -1-e-1 ;②(-1,+∞).
解析试题分析: ⑴由 a=2,b=1得,f (x)=(2+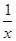 )ex, 定义域为(-∞,0)∪(0,+∞);从而可求得 f ′(x)=
)ex, 定义域为(-∞,0)∪(0,+∞);从而可求得 f ′(x)=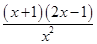 ex, 令f ′(x)=0,得x1=-1,x2=
ex, 令f ′(x)=0,得x1=-1,x2=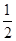 ,列表可求得f (x)的极值.
,列表可求得f (x)的极值.
⑵①当a=1时,g (x)=(x-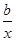 -2)ex,由已知得不等式g (x)≥1在x∈(0,+∞)上恒成立,即b≤x2-2x-
-2)ex,由已知得不等式g (x)≥1在x∈(0,+∞)上恒成立,即b≤x2-2x-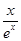 在x∈(0,+∞)上恒成立,从而b≤(x2-2x-
在x∈(0,+∞)上恒成立,从而b≤(x2-2x-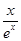 )min x∈(0,+∞),令h(x)=x2-2x-
)min x∈(0,+∞),令h(x)=x2-2x-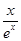 (x>0)利用函数导数求出h(x)的最小值即可.
(x>0)利用函数导数求出h(x)的最小值即可.
②由于g (x)=(ax-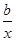 -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=(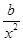 +ax-
+ax-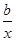 -a)ex; 由g (x)+g ′(x)=0,得(ax-
-a)ex; 由g (x)+g ′(x)=0,得(ax-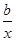 -2a)ex+(
-2a)ex+(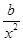 +ax-
+ax-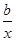 -a)ex=0,整理得2ax3-3ax2-2bx+b=0.
-a)ex=0,整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g (x)+g ′(x)=0成立,等价于存在x>1,2ax3-3ax2-2bx+b=0成立.
注意到a>0,所以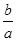 =
=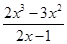 (x>1);设u(x)=
(x>1);设u(x)=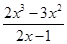 (x>1),则问题等价于
(x>1),则问题等价于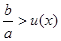 的最小值(或下确界),利用函数导数可判断u(x)在
的最小值(或下确界),利用函数导数可判断u(x)在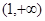 上的单调性可求得
上的单调性可求得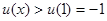 从而可得
从而可得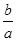 的取值范围为(-1,+∞).
的取值范围为(-1,+∞).
试题解析:⑴当a=2,b=1时,f (x)=(2+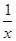 )ex,定义域为(-∞,0)∪(0,+∞).
)ex,定义域为(-∞,0)∪(0,+∞).
所以f ′(x)=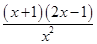 ex.令f ′(x)=0,得x1=-1,x2=
ex.令f ′(x)=0,得x1=-1,x2=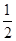 ,列表
,列表x (-∞,-1) -1 (-1,0) (0, 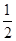 )
)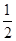
( 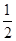 ,+∞)
,+∞)f ′(x) 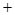
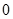
- - 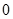
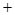
f (x) 
一通百通考必赢系列答案
一线名师夺冠王检测卷系列答案

一路领先优选卷系列答案
一路领先口算题卡系列答案
一课3练课时导练系列答案
一飞冲天课时作业系列答案
一本到位系列答案

阳光课堂星球地图出版社系列答案
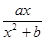 在x=1处取得极值2.
在x=1处取得极值2.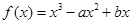 的图象为曲线E.
的图象为曲线E.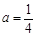 时,求函数y=f(x)的极值;
时,求函数y=f(x)的极值;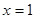 是函数
是函数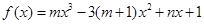 的一个极值点,其中
的一个极值点,其中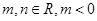 .
.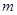 与
与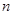 的关系式;
的关系式;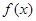 的单调区间;
的单调区间;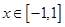 时,函数
时,函数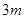 ,求
,求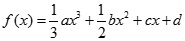 的图像过原点,且在点
的图像过原点,且在点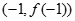 处的切线与
处的切线与 轴平行,对任意
轴平行,对任意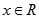 ,都有
,都有 .
. 在点
在点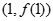 处切线的斜率;
处切线的斜率; 的解析式;
的解析式;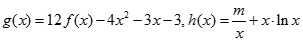 ,对任意
,对任意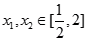 ,都有
,都有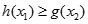 .求实数
.求实数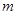 的取值范围.
的取值范围.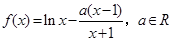 .
.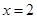 是函数
是函数 的极值点,求曲线
的极值点,求曲线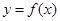 在点
在点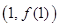 处的切线方程;
处的切线方程;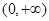 上为单调增函数,求
上为单调增函数,求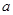 的取值范围;
的取值范围;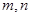 为正实数,且
为正实数,且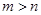 ,求证:
,求证: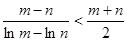 .
. 是函数f(x)=ln(x+1)-x+
是函数f(x)=ln(x+1)-x+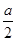 x2的一个极值点。
x2的一个极值点。