题目内容
动圆C经过点F(1,0),并且与直线x=-1相切,若动圆C与直线y=x+2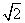 +1总有公共点,则圆C的面积( )
+1总有公共点,则圆C的面积( )
A.有最大值8π B.有最小值2π
C.有最小值3π D.有最小值4π
D

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
动圆C经过点F(1,0),并且与直线x=-1相切,若动圆C与直线y=x+2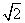 +1总有公共点,则圆C的面积( )
+1总有公共点,则圆C的面积( )
A.有最大值8π B.有最小值2π
C.有最小值3π D.有最小值4π
D

 名校课堂系列答案
名校课堂系列答案