题目内容
设Sn为等比数列{an}的前n项和,8a2+a5=0,则 =
=
- A.-11
- B.-8
- C.5
- D.11
C
分析:由等比数列的前n项和公式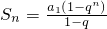 ,故
,故 =
= =1+q2,由此知,应该有方程8a2+a5=0求出q的值,再代入求值,选出正确选项
=1+q2,由此知,应该有方程8a2+a5=0求出q的值,再代入求值,选出正确选项
解答:∵Sn为等比数列{an}的前n项和,8a2+a5=0
∴8a1q+a1q4=0
又数列是等比数列,首项不为0
∴8q+q4=0,又q不为零,故有q=-2
∴ =
= =
= =5
=5
故选C
点评:本题考查等比数列的性质,解题的关键是由8a2+a5=0求出公比q的值,再由等比数列的求和公式将 用q表示出来,即可求出值,本题考查了转化的思想及计算能力,
用q表示出来,即可求出值,本题考查了转化的思想及计算能力,
分析:由等比数列的前n项和公式
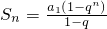 ,故
,故 =
= =1+q2,由此知,应该有方程8a2+a5=0求出q的值,再代入求值,选出正确选项
=1+q2,由此知,应该有方程8a2+a5=0求出q的值,再代入求值,选出正确选项解答:∵Sn为等比数列{an}的前n项和,8a2+a5=0
∴8a1q+a1q4=0
又数列是等比数列,首项不为0
∴8q+q4=0,又q不为零,故有q=-2
∴
 =
= =
= =5
=5故选C
点评:本题考查等比数列的性质,解题的关键是由8a2+a5=0求出公比q的值,再由等比数列的求和公式将
 用q表示出来,即可求出值,本题考查了转化的思想及计算能力,
用q表示出来,即可求出值,本题考查了转化的思想及计算能力, 
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
设Sn为等比数列{an}的前n项和,已知:5S4=a5+2,5S3=a4+2,则公比q=( )
| A、3 | B、4 | C、5 | D、6 |