题目内容
(10分) 已知函数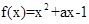
在区间
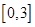上有最小值-2,求实数a 的值
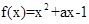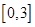在区间上有最小值-2,求实数a 的值a="-2," 符合题意 。
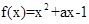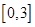考查二次函数在闭区间上的最值问题中的动轴定区间上的最值问题，体现了分类讨论和运动变化的思想方法，属中档题，因为函数在区间上有最小值-2，那么对函数进行配方，对对称轴是否在区间内进行讨论，从而可知函数在何处取得最小值，解出相应的a的值．
解：
,……….1分
(1)当
,即
,函数
在区间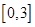上是增函数,此时, 的最小值为
,不符题意,舍去…….4分
(2)当
即
,函数函数在区间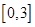上是减函数, 的最小值为
可得a=
,这与矛盾; 不符题意,舍去……..7分
(3)
,即
时,的最小值为
=-2.可得a="-2," 符合题意 …….10分
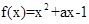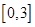在区间上有最小值-2，那么对函数进行配方，对对称轴是否在区间内进行讨论，从而可知函数在何处取得最小值，解出相应的a的值．解：
,……….1分(1)当
,即,函数在区间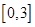上是增函数,此时, 的最小值为,不符题意,舍去…….4分(2)当
即,函数函数在区间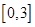上是减函数, 的最小值为可得a=,这与矛盾; 不符题意,舍去……..7分(3)
,即时,的最小值为=-2.可得a="-2," 符合题意 …….10分
练习册系列答案
相关题目
，不等式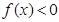
的解集是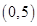
，
的解析式；
，不等式
恒成立，求t的取值范围．
上是减函数，且
。
的值，并求出
和
的取值范围。
。
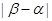的取值范围，并写出当
的解析式。
满足
.
,求
在
的上的值域;
,在
上是单调函数,求
的取值范围.
x2－1的图像开口大小相同，开口方向也相同，y=f(x)的对称轴方程为x=1，图像过点(2, 
)点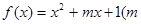
为整数）且关于
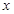的方程
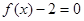在区间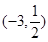
内有两个不同的实根，（1）求整数
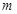的值；（2）若对一切
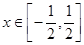，不等式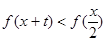
恒成立，求实数
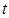的取值范围。
的系数均为整数，若
，且
是方程
两个不等的实数根，则最小正整数
的值为 ．
且
，则
的最小值是______ 
有一个根为
，则
________