题目内容
（选做题）如图，PA与⊙O相切于点A，D为PA的中点，过点D引割线交⊙O于B，C两点，求证：∠DPB=∠DCP．
【答案】分析：先利用切割线定理，再证明△BDP∽△PDC，即可证得结论．
解答：证明：因为PA与圆相切于A，所以DA2=DB•DC，
因为D为PA中点，所以DP=DA，
所以DP2=DB•DC，即
． …（5分）
因为∠BDP=∠PDC，所以△BDP∽△PDC，
所以∠DPB=∠DCP． …（10分）
点评：本题考查三角形的相似，考查切割线定理，解题的关键是证明三角形相似．
解答：证明：因为PA与圆相切于A，所以DA2=DB•DC，
因为D为PA中点，所以DP=DA，
所以DP2=DB•DC，即
． …（5分）因为∠BDP=∠PDC，所以△BDP∽△PDC，
所以∠DPB=∠DCP． …（10分）
点评：本题考查三角形的相似，考查切割线定理，解题的关键是证明三角形相似．
练习册系列答案
名校课堂系列答案
相关题目
（几何证明选讲选做题）如图，PA是圆的切线，A为切点，PBC是圆的割线，且
A．（不等式选讲选做题）函数y=|x+1|+|x-1|的最小值是
（几何证明选讲选做题）如图，PA是圆O的切线，A为切点，PBC是圆O的割线．若
（选做题）如图，PA与⊙O相切于点A，D为PA的中点，过点D引割线交⊙O于B，C两点，求证：∠DPB=∠DCP．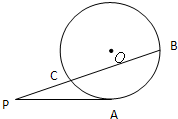
A．（极坐标系与参数方程选做题） 已知圆ρ=3cosθ，则圆截直线