在△ABC中.若sinA-2sinBcosC=0.则△ABC必定是( )A．钝角三角形B．等腰三角形C．直角三角形D．锐角三角形题目和参考答案——青夏教育精英家教网—

题目内容

16．在△ABC中，若sinA-2sinBcosC=0，则△ABC必定是（　　）

A．

钝角三角形

B．

等腰三角形

C．

直角三角形

D．

锐角三角形

分析由已知利用三角形内角和定理，两角和与差的正弦函数公式可得sin（B-C）=0，利用正弦函数的图象和性质可求B=C，即可得解△ABC必定是等腰三角形．

解答解：∵由已知可得：sinA=sin（B+C）=sinBcosC+cosBsinC=2sinBcosC，
∴sin（B-C）=0，
∵B-C∈（-π，π），
∴B=C，
∴△ABC必定是等腰三角形．
故选：B．

点评本题主要考查了三角形内角和定理，两角和与差的正弦函数，正弦函数的图象和性质的应用，考查了转化思想，属于基础题．

练习册系列答案

口算题卡加应用题专项沈阳出版社系列答案

7．一个口袋里装有大小相同的6个小球，其中红色、黄色、绿色的球各2个，现从中任意取出3个小球，其中恰有2个小球同颜色的概率是$\frac{3}{5}$．若取到红球得1分，取到黄球得2分，取到绿球得3分，记变量ξ为取出的三个小球得分之和，则ξ的期望为6．

4．在区间[0，9]上随机取一实数x，则该实数x满足不等式1≤log₂x≤2的概率为（　　）

11．如图，已知圆C的方程为x²+y²=1，P是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1上的一点，过P作圆的两条切线，切点为A，B，则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围为（　　）

[$\frac{3}{2}$，$\frac{9}{2}$]

1．

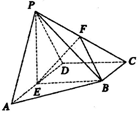在四棱锥P-ABCD中，E为棱AD的中点，PE⊥平面ABCD，AD∥BC，∠ADC=90°，ED=BC=2，EB=3，F为棱PC的中点．
（Ⅰ）求证：PA∥平面BEF；
（Ⅱ）若二面角F-BE-C为60°，求直线PB与平面ABCD所成角的正切值．

8．在直角坐标系xOy中，曲线C₁：$\left\{\begin{array}{l}x=2+\sqrt{7}cosα\\ y=\sqrt{7}sinα\end{array}\right.$（α为参数）．以O为极点，x轴的正半轴为极轴建立极坐标系，曲线C₂的极坐标方程为ρ=8cosθ，直线l的极坐标方程为$θ=\frac{π}{3}（ρ∈R）$．
（Ⅰ）求曲线C₁的极坐标方程与直线l的直角坐标方程；
（Ⅱ）若直线l与C₁，C₂在第一象限分别交于A，B两点，P为C₂上的动点，求△PAB面积的最大值．

5．在△ABC中，∠ACB=60°，BC＞1，AC=AB+$\frac{1}{2}$，当△ABC的周长最短时，BC的长是$\frac{\sqrt{2}}{2}$+1．

10．下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（　　）

试题分类