题目内容
要制作一个如图的框架(单位:m),要求所围成的总面积为19.5(m2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h= AB,tan∠FED=
AB,tan∠FED=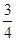 ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.
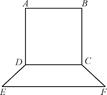
(1)求y关于x的表达式;
(2)如何设计x、y的长度,才能使所用材料最少?
 AB,tan∠FED=
AB,tan∠FED=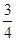 ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.
(1)求y关于x的表达式;
(2)如何设计x、y的长度,才能使所用材料最少?
(1)y=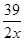 -
-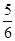 x
x 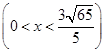 (2)AB=3m,BC=4m
(2)AB=3m,BC=4m
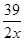 -
-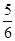 x
x 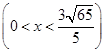 (2)AB=3m,BC=4m
(2)AB=3m,BC=4m(1)如图,在等腰梯形CDEF中,DH是高.
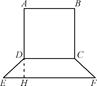
依题意:DH= AB=
AB= x,EH=
x,EH=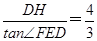 ×
× x=
x=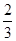 x,
x,
∴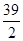 =xy+
=xy+
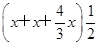 x=xy+
x=xy+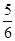 x2,∴y=
x2,∴y=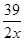 -
-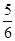 x.
x.
∵x>0,y>0,∴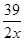 -
-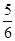 x>0,解之得0<x<
x>0,解之得0<x<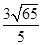 .
.
∴所求表达式为y=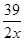 -
-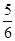 x
x 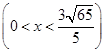 .
.
(2)在Rt△DEH中,∵tan∠FED=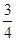 ,∴sin∠FED=
,∴sin∠FED=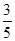 ,
,
∴DE=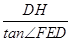 =
= x×
x×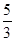 =
=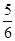 x,
x,
∴l=(2x+2y)+2×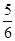 x+
x+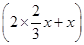 =2y+6x=
=2y+6x=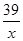 -
-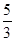 x+6x=
x+6x=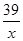 +
+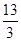 x≥2
x≥2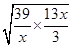 =26,
=26,
当且仅当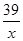 =
=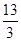 x,即x=3时取等号,
x,即x=3时取等号,
此时y=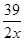 -
-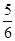 x=4,
x=4,
∴AB=3m,BC=4m时,能使整个框架所用材料最少.

依题意:DH=
 AB=
AB= x,EH=
x,EH=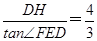 ×
× x=
x=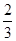 x,
x,∴
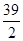 =xy+
=xy+
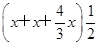 x=xy+
x=xy+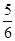 x2,∴y=
x2,∴y=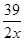 -
-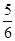 x.
x.∵x>0,y>0,∴
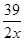 -
-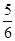 x>0,解之得0<x<
x>0,解之得0<x<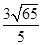 .
.∴所求表达式为y=
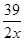 -
-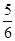 x
x 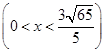 .
.(2)在Rt△DEH中,∵tan∠FED=
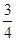 ,∴sin∠FED=
,∴sin∠FED=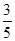 ,
,∴DE=
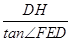 =
= x×
x×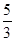 =
=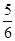 x,
x,∴l=(2x+2y)+2×
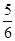 x+
x+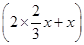 =2y+6x=
=2y+6x=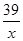 -
-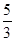 x+6x=
x+6x=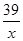 +
+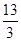 x≥2
x≥2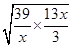 =26,
=26,当且仅当
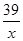 =
=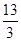 x,即x=3时取等号,
x,即x=3时取等号,此时y=
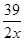 -
-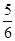 x=4,
x=4,∴AB=3m,BC=4m时,能使整个框架所用材料最少.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
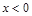 ,则
,则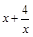 的最大值为 。
的最大值为 。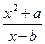 (b≠1)在x=1处有极值,则ab的最大值等于 。
(b≠1)在x=1处有极值,则ab的最大值等于 。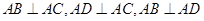 ,
,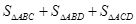 的最大值是 _______ .
的最大值是 _______ .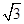 ,则该三角形的面积的最大值为 .
,则该三角形的面积的最大值为 .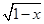 +
+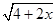 的最大值.
的最大值.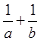 取最小值的实数对(a,b)是
取最小值的实数对(a,b)是