题目内容
从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且其长轴端点A及短轴端点B的连线AB平行于OM.(1)求椭圆的离心率;
(2)若Q是椭圆上任意一点,F2是右焦点,求∠F1QF2的取值范围.
解:(1)∵MF1⊥x轴,∴xM=-c.

代入椭圆方程得yM=![]() ,∴kOM=-
,∴kOM=-![]() .
.
又∵kAB=-![]() 且OM∥AB,
且OM∥AB,
∴-![]() .故b=c.∴a2=b2+c2=2c2.
.故b=c.∴a2=b2+c2=2c2.
∴![]() .
.
(2)设|QF1|=r1,|QF2|=r2,∠F1QF2=θ.
∵r1+r2=2a,|F1F2|=2c,
∵e=![]() ,∴c2=
,∴c2=![]() a2.
a2.
∴cosθ=![]()
=![]()
=![]() -1≥
-1≥ -1=0.
-1=0.
当且仅当r1=r2时,上式等号成立.
∴0≤cosθ≤1,θ∈[0,![]() ],即∠F1QF2∈[0,
],即∠F1QF2∈[0, ![]() ].
].

练习册系列答案
相关题目
 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围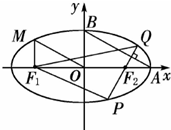 (普通班)如图所示,从椭圆
(普通班)如图所示,从椭圆 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭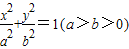 上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且
上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且 ∥
∥ ,则a,b,c必满足 .
,则a,b,c必满足 .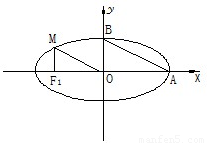
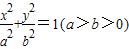 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭