题目内容
(普通班)如图所示,从椭圆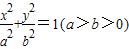 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB∥OM.
(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点,F2是右焦点,F1是左焦点,求∠F1QF2的取值范围.

【答案】分析:(1)首先根据MF1⊥x轴,AB∥OM,得到Rt△OMF1∽Rt△ABO,从而得到比例线段: .再根据点M在椭圆上,
.再根据点M在椭圆上,
求出M的纵坐标,得出MF1= ,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e;
,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e;
(2)当点Q与椭圆长轴的端点重合时,∠F1QF2的大小为零;当点Q不与椭圆长轴的端点重合时,设∠F1QF2的大小为θ,
在△F1QF2中,利用余弦定理,结合基本不等式和椭圆的定义,可以证出4a2-4c2≤2a2(1+cosθ),结合(1)的结论
a2=2c2,可以证出cosθ≥0,从而得到0<θ≤ .最后综合,得到
.最后综合,得到 ,即为∠F1QF2的取值范围.
,即为∠F1QF2的取值范围.
解答:解:(1)∵MF1⊥x轴,AB∥OM,
∴Rt△OMF1∽Rt△ABO⇒ …(*)
…(*)
设点M(-c,y1),代入椭圆方程 ,
,
得 ,解之得y1=
,解之得y1= (舍负),所以MF1=
(舍负),所以MF1= ,
,
又∵AO=a,BO=b,OF1=c,
∴将AO、BO、MF1、OF1的长代入(*)式,得 ,
,
∴b=c,得到b2=c2,即a2-c2=c2,所以a2=2c2,
∴离心率e满足e2= ,可得
,可得 (舍负)(8分)
(舍负)(8分)
(2)分两种情况加以讨论
①当点Q与椭圆长轴的端点重合时,∠F1QF2的大小为零;
②当点Q不与椭圆长轴的端点重合时,设∠F1QF2的大小为θ,则
在△F1QF2中,
即 ,
,
将F1F2=2c,QF1+QF2=2a代入,得4c2=4a2-2QF1•QF2(1+cosθ),
∴4a2-4c2=2QF1•QF2(1+cosθ),
∵QF1•QF2≤ =a2,即得2QF1•QF2(1+cosθ)≤2a2(1+cosθ),
=a2,即得2QF1•QF2(1+cosθ)≤2a2(1+cosθ),
∴4a2-4c2≤2a2(1+cosθ),结合(1)的结论a2=2c2,
∴2a2≤2a2(1+cosθ)⇒cosθ≥0,
∵θ∈(0,π)
∴0<θ≤ ,
,
综上所述, ,即∠F1QF2的取值范围是
,即∠F1QF2的取值范围是 (14分)
(14分)
点评:本题结合一个特殊的椭圆,以求椭圆的离心率和焦点三角形中角的取值范围为载体,着重考查了椭圆的基本概念、余弦定理和基本不等式等知识点,属于中档题.
 .再根据点M在椭圆上,
.再根据点M在椭圆上,求出M的纵坐标,得出MF1=
 ,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e;
,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e;(2)当点Q与椭圆长轴的端点重合时,∠F1QF2的大小为零;当点Q不与椭圆长轴的端点重合时,设∠F1QF2的大小为θ,
在△F1QF2中,利用余弦定理,结合基本不等式和椭圆的定义,可以证出4a2-4c2≤2a2(1+cosθ),结合(1)的结论
a2=2c2,可以证出cosθ≥0,从而得到0<θ≤
 .最后综合,得到
.最后综合,得到 ,即为∠F1QF2的取值范围.
,即为∠F1QF2的取值范围.解答:解:(1)∵MF1⊥x轴,AB∥OM,
∴Rt△OMF1∽Rt△ABO⇒
 …(*)
…(*)设点M(-c,y1),代入椭圆方程
 ,
,得
 ,解之得y1=
,解之得y1= (舍负),所以MF1=
(舍负),所以MF1= ,
,又∵AO=a,BO=b,OF1=c,
∴将AO、BO、MF1、OF1的长代入(*)式,得
 ,
,∴b=c,得到b2=c2,即a2-c2=c2,所以a2=2c2,
∴离心率e满足e2=
 ,可得
,可得 (舍负)(8分)
(舍负)(8分) (2)分两种情况加以讨论
①当点Q与椭圆长轴的端点重合时,∠F1QF2的大小为零;
②当点Q不与椭圆长轴的端点重合时,设∠F1QF2的大小为θ,则
在△F1QF2中,

即
 ,
,将F1F2=2c,QF1+QF2=2a代入,得4c2=4a2-2QF1•QF2(1+cosθ),
∴4a2-4c2=2QF1•QF2(1+cosθ),
∵QF1•QF2≤
 =a2,即得2QF1•QF2(1+cosθ)≤2a2(1+cosθ),
=a2,即得2QF1•QF2(1+cosθ)≤2a2(1+cosθ),∴4a2-4c2≤2a2(1+cosθ),结合(1)的结论a2=2c2,
∴2a2≤2a2(1+cosθ)⇒cosθ≥0,
∵θ∈(0,π)
∴0<θ≤
 ,
,综上所述,
 ,即∠F1QF2的取值范围是
,即∠F1QF2的取值范围是 (14分)
(14分)点评:本题结合一个特殊的椭圆,以求椭圆的离心率和焦点三角形中角的取值范围为载体,着重考查了椭圆的基本概念、余弦定理和基本不等式等知识点,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
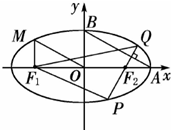 (普通班)如图所示,从椭圆
(普通班)如图所示,从椭圆 上一点M向
上一点M向 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点 ,且它的长轴端点A及短轴端点B的连线
,且它的长轴端点A及短轴端点B的连线 .
.
 是右焦点,
是右焦点, 的取值范围;
的取值范围;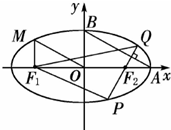 (普通班)如图所示,从椭圆
(普通班)如图所示,从椭圆 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭