题目内容
等腰三角形ABC的腰AB上的中线CD的长为2,则△ABC周长的最大值 .
【答案】分析:设等腰三角形ABC的腰AB=AC长为2x,底为y,根据三角形中线公式,可以得到2x2+y2=8,进而由柯西不等式可以得到△ABC周长4x+y的取值范围.
解答:解:设等腰三角形ABC的腰AB=AC长为2x,底为y,
∵腰AB上的中线CD的长为2,
由中线公式可得2x2+y2=8①
则周长C=4x+y②
由柯西不等式就可得
(2x2+y2)(8+1)≥(4x+y)2
所以4x+y≤6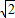
当且仅当2x2=8y2,即x=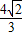 ,y=
,y=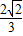 时
时
△ABC周长取最大值为6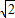
故答案为:6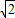
点评:本题考查的知识点是柯西不等式,其中根据三角形中线公式求出等腰三角形ABC的腰AB=AC长为2x,底为y时,2x2+y2=8是解答的关键.
解答:解:设等腰三角形ABC的腰AB=AC长为2x,底为y,
∵腰AB上的中线CD的长为2,
由中线公式可得2x2+y2=8①
则周长C=4x+y②
由柯西不等式就可得
(2x2+y2)(8+1)≥(4x+y)2
所以4x+y≤6
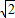
当且仅当2x2=8y2,即x=
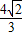 ,y=
,y=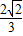 时
时△ABC周长取最大值为6
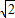
故答案为:6
点评:本题考查的知识点是柯西不等式,其中根据三角形中线公式求出等腰三角形ABC的腰AB=AC长为2x,底为y时,2x2+y2=8是解答的关键.

练习册系列答案
相关题目