题目内容
19.(1)已知|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2. 若$\overrightarrow{a}$•$\overrightarrow{b}$=-3,则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为$\frac{2π}{3}$.(2)已知$\overrightarrow{a}$=(m-2,-3),$\overrightarrow{b}$=(-1,m),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则m=3或-1.
分析 (1)两个向量数量积的定义,求得两个向量夹角的余弦值,可得两个向量夹角.
(2)利用两个向量共线的性质,求得m的值.
解答 解:(1)设$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为θ,θ∈[0,π],∵已知|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•$\overrightarrow{b}$=-3,
∴$\overrightarrow{a}•\overrightarrow{b}$=3•2•cosθ=-3,∴cosθ=-$\frac{1}{2}$,∴θ=$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$.
(2)∵已知$\overrightarrow{a}$=(m-2,-3),$\overrightarrow{b}$=(-1,m),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则m(m-2)-(-3)(-1)=0,(m-3)(m+1)=0,
∴m=3,或m=-1,
故答案为:3或-1.
点评 本题主要考查两个向量数量积的定义,两个向量共线的性质,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
10.已知f(x)=x3-3x+2+m(m>0).在区间[0,2]上存在三个不同的实数a,b,c,使得以f(a),f(b),f(c)为边长的三角形是直角三角形,则m的取值范围是( )
| A. | m>4+4$\sqrt{2}$ | B. | 0<m<2+2$\sqrt{2}$ | C. | 4-4$\sqrt{2}$<m<4+4$\sqrt{2}$ | D. | 0<m<4+4$\sqrt{2}$ |
7.下列几种推理过程是演绎推理的是( )
| A. | 5和ln3可以比较大小 | |
| B. | 由平面三角形的性质,推测空间四面体的性质 | |
| C. | 东升高中高二年级有15个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人 | |
| D. | 预测股票走势图 |
14.已知函数f(x)=alnx+blog2x+1,f(2017)=3,则$f(\frac{1}{2017})$等于( )
| A. | -1 | B. | 2 | C. | -2 | D. | $\frac{1}{4}$ |
4.设集合U={0,1,2,3,4,5},A={1,2},B={x∈Z|x2-5x+4<0},则(∁UA)∩(∁UB)=( )
| A. | {0,1,2,3} | B. | {5} | C. | {1,2,4} | D. | {0,4,5} |
11.三棱锥S-ABC中,AB=BC=AC=2,SC=4,SA=SB,SC与平面ABC所成角的余弦值是$\frac{{\sqrt{3}}}{3}$,若S,A,B,C都在同一球面上,则该球的表面积是( )
| A. | 4π | B. | 8π | C. | 16π | D. | 64π |
8.运行如图所示的程序框图,则输出的a、b、c满足( )
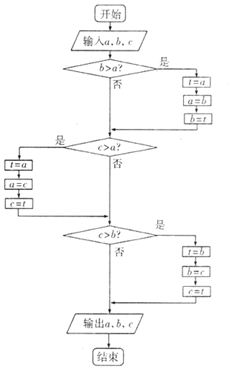

| A. | c≤b≤a | B. | a≤b≤c | C. | a≤c≤b | D. | b≤c≤a |