题目内容
已知向量 ,
, 的夹角为60°,且
的夹角为60°,且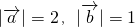 ,则
,则 与
与 的夹角等于
的夹角等于
- A.150°
- B.90°
- C.60°
- D.30°
C
分析:根据题意并结合向量数量积的运算性质,分别算出| |、|
|、| |和
|和 与
与 的数量积,最后用向量夹角公式即可得到
的数量积,最后用向量夹角公式即可得到 与
与 的夹角大小.
的夹角大小.
解答:由题意可得 =2×1cos60°=1,
=2×1cos60°=1,
设向量 与
与 的夹角等于θ,
的夹角等于θ,
∵( )2=
)2= -2
-2 +
+ =4-2×1+1=3,(
=4-2×1+1=3,( )2=
)2= +4
+4 +4
+4 =4+4×1+4=12,
=4+4×1+4=12,
∴| |=
|= ,|
,| |=
|= =2
=2
而( )(
)( )=
)= +
+ -2
-2 =4+1-2=3
=4+1-2=3
由此可得cosθ= =
= =
= .
.
再由 0°≤θ≤180°,可得θ=60°,
故选:C
点评:题主要考查两个向量的夹角公式,两个向量数量积公式,求向量的模的方法,属于中档题.
分析:根据题意并结合向量数量积的运算性质,分别算出|
 |、|
|、| |和
|和 与
与 的数量积,最后用向量夹角公式即可得到
的数量积,最后用向量夹角公式即可得到 与
与 的夹角大小.
的夹角大小.解答:由题意可得
 =2×1cos60°=1,
=2×1cos60°=1,设向量
 与
与 的夹角等于θ,
的夹角等于θ,∵(
 )2=
)2= -2
-2 +
+ =4-2×1+1=3,(
=4-2×1+1=3,( )2=
)2= +4
+4 +4
+4 =4+4×1+4=12,
=4+4×1+4=12,∴|
 |=
|= ,|
,| |=
|= =2
=2
而(
 )(
)( )=
)= +
+ -2
-2 =4+1-2=3
=4+1-2=3由此可得cosθ=
 =
= =
= .
.再由 0°≤θ≤180°,可得θ=60°,
故选:C
点评:题主要考查两个向量的夹角公式,两个向量数量积公式,求向量的模的方法,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 ,
, 的夹角为
的夹角为 ,且|
,且| |=
|= ,|
,| |=2.在△ABC中,
|=2.在△ABC中, =2
=2 +2
+2 ,
, =2
=2 -6
-6 ,D为BC边的中点,则|
,D为BC边的中点,则| |= .
|= .