题目内容
设二次函数
 满足条件:
满足条件:
① ,②
,② ;③
;③ 在
在 上的最小值为
上的最小值为 .
.
(I)求 的值;
的值;
(II)求 的解析式;
的解析式;
(III)求最大值 ,使得存在
,使得存在 ,只要
,只要 ,都有
,都有 成立.
成立.
解:(I) ∵ 在
在 上恒成立,
上恒成立,
∴
即 .
.
(II)∵ ,∴函数图象关于直线
,∴函数图象关于直线 对称,
对称,
∴
∵ ,∴
,∴
又∵ 在
在 上的最小值为
上的最小值为 ,∴
,∴ ,即
,即 ,
,
由 解得
解得 ,
,
∴ ;
;
(III)∵当 时,
时, 
 恒成立,∴
恒成立,∴ 且
且 ,
,
由 得,解得
得,解得
由 得:
得: ,
,
解得
∵ ,∴
,∴
当 时,对于任意
时,对于任意 ,恒有
,恒有 ,
,
∴ 的最大值为
的最大值为 .
.
另解:(酌情给分) 且
且

 在
在 上恒成立
上恒成立

∵ 在
在 上递减,∴
上递减,∴ ,
,
∵ 在
在 上递减,
上递减,
∴
∴ ,∴
,∴ ,
, ,
,
∵ ,∴
,∴ ,
,
∴ ,∴
,∴ 的最大值为
的最大值为

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的两条渐近线的方程为
的两条渐近线的方程为  ( )
( ) (B)
(B) (C)
(C)  (D)
(D) 
 在边长为
在边长为 的正方形的边上运动,设
的正方形的边上运动,设 是
是 的中点,则当
的中点,则当
 运动时,点
运动时,点 与△
与△ 的面积
的面积 的函数关系为
的函数关系为 ,则
,则

 (其中
(其中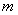 为整数),则
为整数),则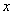 最近的整数,记作
最近的整数,记作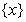 ,即
,即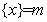 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数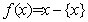 的四个判断:
的四个判断: 的定义域是
的定义域是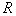 ,值域是
,值域是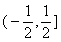 ;
;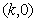 是
是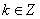 ;
;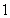 ;
;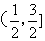 上是增函数.
上是增函数. ,
, ,
, 共线,则实数
共线,则实数 .
. ,且
,且 ,则
,则
 平面
平面 ,且直线
,且直线 平面
平面 ,则
,则
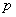 :函数
:函数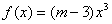 在
在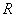 上是减函数,
上是减函数,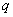 :
: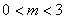 ,则
,则 B.
B.  C.
C.  D.
D. 
