Question

（1）用“五点法”作函数y=2sin（2x－），x∈R的图象，并指出这个函数的振幅、周期和初相；

（2）怎样由y=sinx的图象，得到y=2sin（2x－）的图象？

Answer 1

（1）解：

列表：

x
	0		π		2π
	0	2	0	－2	0

描点连线：

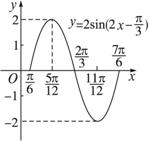
把函数在长度为一个周期的简图中向左右扩展，就得到

，x∈R的简图.振幅A=2，周期，初相φ=.

（2）解法一：先把函数y=sinx的图象上所有的点向右平移个单位，得到函数的图象；再把图象上所有点的横坐标缩短到原来的倍?（纵坐标不变），得到函数的图象；最后把图象上所有点的纵坐标伸长到原来的2倍（横坐标不变）得到，x∈R的图象.

解法二：先把y=sinx图象上所有点的横坐标缩短到原来的倍（纵坐标不变），得到函数y=sin2x的图象；再把y=sin2x的图象上所有的点向右平移个单位，得到函数的图象；最后把图象上所有点的纵坐标伸长到原来的2倍（横坐标不变），就得到函数，x∈R的图象.

方法归纳 用五点法作图的关键是把相位（ωx+φ）视为一个整体，令它依次取0，，π，，2π这些值，解出相应的x值，得到各个点的横坐标.

深化升华 先相位，再周期变换，同先周期，后相位变换一样，函数y=sinx图象上的点（0，0）被变换成了点（，0）.但要注意平移的单位是不同的，先相位后周期，平移的单位为|φ|；先周期，后相位，平移的单位为.