题目内容
已知函数f(x)=x3+ax2+bx+c在x=-
与x=1时都取得极值
(1)求a,b的值和函数f(x)的单调区间;
(2)若直线y=b与函数y=f(x)的图象有3个交点,求c的取值范围;
(3)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
| 2 |
| 3 |
(1)求a,b的值和函数f(x)的单调区间;
(2)若直线y=b与函数y=f(x)的图象有3个交点,求c的取值范围;
(3)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)根据所给的函数的解析式,对函数求导,使得导函数等于0,得到关于a,b的关系式,解方程组即可,写出函数的解析式.
(2)对函数求导,求出极值,令极大值大于b,极小值小于b,解此不等式组即可求得结果.
(3)将不等式不等式f(x)<c2恒成立,转化为x∈[-1,2],不等式fmax(x)<c2恒成立,求函数的最大值即可得到结论.
(2)对函数求导,求出极值,令极大值大于b,极小值小于b,解此不等式组即可求得结果.
(3)将不等式不等式f(x)<c2恒成立,转化为x∈[-1,2],不等式fmax(x)<c2恒成立,求函数的最大值即可得到结论.
解答:
解:(1)∵f(x)=x3+ax2+bx+c,∴f′(x)=3x2+2ax+b,
∵函数f(x)在x=-
与x=1时都取得极值,
∴f′(-
)=0,f′(1)=0,
即f′(-
)=
-
+b=0,f′(1)=3+2a+b=0
得a=-
,b=-2,
经检验,a=,b=-2符合题意.
则f(x)=x3-
x2-2x+c,
∴f′(x)=3x2-x-2=(3x+2)(x-1),
列表
,则函数的单调增区间为(-∞,-
)和(1,+∞).
(2)由(1)可得函数f(x)的极大值为f(-
)=
+c,极小值f(1)=-
+c,
要使y=b=-2与函数y=f(x)的图象有3个交点,
则
,即
,即-
<c<-
,
即c的取值范围是-
<c<-
.
(3)对x∈[-1,2],不等式f(x)<c2恒成立,
则等价为对x∈[-1,2],不等式fmax(x)<c2恒成立,
∵f(-1)=
+c,f(2)=2+c,函数f(x)的极大值为f(-
)=
+c,极小值f(1)=-
+c,
∴函数的最大值为f(2)=2+c,
要使不等式fmax(x)<c2恒成立,
则2+c<c2,即c2-c-2>0,解得c>2或c<-1,
即c的取值范围是c>2或c<-1.
∵函数f(x)在x=-
| 2 |
| 3 |
∴f′(-
| 2 |
| 3 |
即f′(-
| 2 |
| 3 |
| 12 |
| 9 |
| 4a |
| 3 |
得a=-
| 1 |
| 2 |
经检验,a=,b=-2符合题意.
则f(x)=x3-
| 1 |
| 2 |
∴f′(x)=3x2-x-2=(3x+2)(x-1),
列表
| x | (-∞,-
| -
| (-
| 1 | (1,+∞) | ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
| 2 |
| 3 |
(2)由(1)可得函数f(x)的极大值为f(-
| 2 |
| 3 |
| 22 |
| 27 |
| 3 |
| 2 |
要使y=b=-2与函数y=f(x)的图象有3个交点,
则
|
|
| 76 |
| 27 |
| 1 |
| 2 |
即c的取值范围是-
| 76 |
| 27 |
| 1 |
| 2 |
(3)对x∈[-1,2],不等式f(x)<c2恒成立,
则等价为对x∈[-1,2],不等式fmax(x)<c2恒成立,
∵f(-1)=
| 1 |
| 2 |
| 2 |
| 3 |
| 22 |
| 27 |
| 3 |
| 2 |
∴函数的最大值为f(2)=2+c,
要使不等式fmax(x)<c2恒成立,
则2+c<c2,即c2-c-2>0,解得c>2或c<-1,
即c的取值范围是c>2或c<-1.
点评:本题主要考查导数的应用,根据函数极值和导数之间的关系求出函数的解析式是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
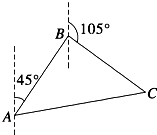 如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.
如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.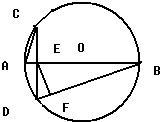 如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.
如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.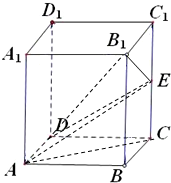 在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点
在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点