题目内容
如图，点P是线段AB上的一点，且AP：PB=m：n，点O是直线AB外一点，设| OA |
| a |
| OB |
| b |
| a |
| b |
| OP |
分析：利用共线向量定理和向量数乘的定义建立共线向量之间的倍数关系是解决本题的关键．注意在转化过程中向量加法，减法的三角形法则的运用，将未知向量用已知向量表示出来．
解答：解：由题意，
=
-
=
-
，
又因为AP：PB=m：n，
因此
=
，
因此，
=
+
=
+
(
-
)=
+
．
| AB |
| OB |
| OA |
| b |
| a |
又因为AP：PB=m：n，
因此
| AP |
| m |
| m+n |
| AB |
因此，
| OP |
| OA |
| AP |
| a |
| m |
| m+n |
| b |
| a |
| m |
| m+n |
| b |
| n |
| m+n |
| a |
点评：本题考查向量基底的思想，考查用已知向量表示未知向量的思想，关键要用向量的线性运算建立未知向量和已知向量的关系，考查学生的转化和化归思想．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
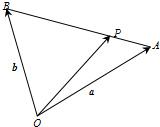如右图，设点P是线段AB靠近A的四等分点，若
如图，点A是⊙O内一个定点，点B是⊙O上一个动点，⊙O的半径为r（r为定值），点P是线段AB的垂直平分线与OB的交点，则点P的轨迹是（ ）
=
，
=
，则
= ，（用a、b表示）