题目内容
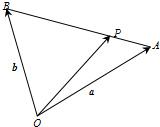如右图，设点P是线段AB靠近A的四等分点，若| OA |
| a |
| OB |
| b |
| OP |
分析：由向量加法的三角形法则，我们易得
=
+
，而根据点P是线段AB靠近A的四等分点，结合共线向量的性质，我们易得
=
，再由向量减法的三角形法则，
=
-
，我们易将
分解为用
与
表示的形式，再由
=
，
=
，即可得到答案．
| OP |
| OA |
| AP |
| AP |
| 1 |
| 4 |
| AB |
| AB |
| OB |
| OA |
| OP |
| OB |
| OA |
| OA |
| a |
| OB |
| b |
解答：解：∵点P是线段AB靠近A的四等分点，
∴
=
∴
=
+
=
+
=
+
（
-
）
=
+
=
+
故答案为：
+
∴
| AP |
| 1 |
| 4 |
| AB |
∴
| OP |
| OA |
| AP |
| OA |
| 1 |
| 4 |
| AB |
=
| OA |
| 1 |
| 4 |
| OB |
| OA |
=
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
=
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
故答案为：
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
点评：本题考查的知识点是平面向量的基本定理，向量加减法的三角形法则，共线（平行）向量的性质等，其中利用向量加减法的三角形法则将向量
分解为用
与
表示的形式，是解答本题的关键．
| OP |
| OB |
| OA |
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
相关题目
=
，
=
，则
= ，（用a、b表示）