题目内容
已知函数f(x)=x3-ax2+3x+1.
(Ⅰ)当a=5时,求曲线y=f(x)在点(2,f(2)处的切线方程;
(Ⅱ)在(Ⅰ)的条件下,求函数f(x)的单调区间;
(Ⅲ)若f(x)在区间(2,3)内至少有一个极值点,求实数a的取值范围.
(Ⅰ)当a=5时,求曲线y=f(x)在点(2,f(2)处的切线方程;
(Ⅱ)在(Ⅰ)的条件下,求函数f(x)的单调区间;
(Ⅲ)若f(x)在区间(2,3)内至少有一个极值点,求实数a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(Ⅰ)当a=5时,f(x)=x3-5x2+3x+1,求导f′(x)=3x2-10x+3=(3x-1)(x-3),从而求切线方程;
(Ⅱ)在(Ⅰ)的条件下,f′(x)=3x2-10x+3=(3x-1)(x-3),由导数的正负确定函数f(x)的单调区间;
(Ⅲ)f(x)在区间(2,3)内至少有一个极值点可转化为f′(x)=3x2-2ax+3=0在(2,3)内有解且f′(x)=3x2-2ax+3在(2,3)上有正有负,从而求实数a的取值范围.
(Ⅱ)在(Ⅰ)的条件下,f′(x)=3x2-10x+3=(3x-1)(x-3),由导数的正负确定函数f(x)的单调区间;
(Ⅲ)f(x)在区间(2,3)内至少有一个极值点可转化为f′(x)=3x2-2ax+3=0在(2,3)内有解且f′(x)=3x2-2ax+3在(2,3)上有正有负,从而求实数a的取值范围.
解答:
解:(Ⅰ)当a=5时,f(x)=x3-5x2+3x+1,
f′(x)=3x2-10x+3=(3x-1)(x-3),
f(2)=8-5×4+3×2+1=-5,
f′(2)=12-20+3=-5,
故曲线y=f(x)在点(2,f(2)处的切线方程为
y+5=-5(x-2),
即5x+y-5=0;
(Ⅱ)在(Ⅰ)的条件下,
f′(x)=3x2-10x+3=(3x-1)(x-3),
则函数f(x)的单调增区间为(-∞,
),(3,+∞);
单调减区间为[
,3];
(Ⅲ)f′(x)=3x2-2ax+3,
①当
≤2或
≥3,即a≤6或a≥9时,
f′(x)在[2,3]上单调,
故有f′(2)•f′(3)<0,
即(12-4a+3)(27-6a+3)<0,
故
<a<5,
②当2<
<3,即6<a<9时,
f′(2)>0或f′(3)>0,且f′(
)<0;
无解;
故若f(x)在区间(2,3)内至少有一个极值点,
实数a的取值范围为(
,5).
f′(x)=3x2-10x+3=(3x-1)(x-3),
f(2)=8-5×4+3×2+1=-5,
f′(2)=12-20+3=-5,
故曲线y=f(x)在点(2,f(2)处的切线方程为
y+5=-5(x-2),
即5x+y-5=0;
(Ⅱ)在(Ⅰ)的条件下,
f′(x)=3x2-10x+3=(3x-1)(x-3),
则函数f(x)的单调增区间为(-∞,
| 1 |
| 3 |
单调减区间为[
| 1 |
| 3 |
(Ⅲ)f′(x)=3x2-2ax+3,
①当
| a |
| 3 |
| a |
| 3 |
f′(x)在[2,3]上单调,
故有f′(2)•f′(3)<0,
即(12-4a+3)(27-6a+3)<0,
故
| 15 |
| 4 |
②当2<
| a |
| 3 |
f′(2)>0或f′(3)>0,且f′(
| a |
| 3 |
无解;
故若f(x)在区间(2,3)内至少有一个极值点,
实数a的取值范围为(
| 15 |
| 4 |
点评:本题考查了导数的综合应用,同时考查了分类讨论的数学思想,属于难题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
双曲线C:
-
=1(a>0,b>0)的左右焦点分别为F1(-c,0),F2(c,0),M是双曲线上的一点,且满足
•
+2a2=0,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| F2M |
A、(1,
| ||
B、(
| ||
C、(1,
| ||
D、(
|
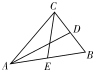 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E分别是BC、AB的中点,P是△ABC(包括边界)内任一点,则
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E分别是BC、AB的中点,P是△ABC(包括边界)内任一点,则| AD |
| EP |
| A、[-7,7] |
| B、[-8,8] |
| C、[-9,9] |
| D、[-10,O] |
