题目内容
1.某校设计了一个实验考察方案:考生从6道备选题中随机抽取3道题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中的2道题便可通过.己知6道备选题中考生甲有4道能正确完成,2道题不能完成;考生乙每题正确完成的概率都是$\frac{2}{3}$,且每题正确完成与否互不影响.(I) 求甲考生通过的概率;
(II) 求甲、乙两考生正确完成题数的概率分布列,和甲、乙两考生的数学期望;
(Ⅲ)请分析比较甲、乙两考生的实验操作能力.
分析 (Ⅰ)考生甲要通过实验考查,必须正确完成至少2道,利用对立事件概率计算公式能求出甲考生通过的概率.
(Ⅱ)确定考生甲正确完成实验操作的题目个数的取值,求出相应的概率,可得考生甲正确完成题目个数ξ的分布列和数学期望;乙两考生正确完成题数Y的可能取值为0,1,2,3,且Y~B(3,$\frac{2}{3}$),由此能求出考生乙正确完成题目个数ξ的分布列和数学期望.
(Ⅲ)设考生乙正确完成实验操作的题目个数为η,求出相应的期望与方差,比较,即可得出结论.
解答 解:(Ⅰ)∵考生从6道备选题中随机抽取3道题,按照题目要求独立完成全部实验操作,
规定:至少正确完成其中的2道题便可通过.
己知6道备选题中考生甲有4道能正确完成,2道题不能完成,
∴甲考生通过的概率P=1-$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{4}{5}$.
(Ⅱ)由题意知甲考生正确完成题数X的可能取值为1,2,3,
P(X=1)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(X=3)=$\frac{{C}_{4}^{2}{C}_{2}^{0}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴X的可能取值为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
乙两考生正确完成题数Y的可能取值为0,1,2,3,
P(Y=0)=${C}_{3}^{0}$($\frac{1}{3}$)3=$\frac{1}{27}$,
P(Y=1)=${C}_{3}^{1}(\frac{2}{3})(\frac{1}{3})^{2}$=$\frac{6}{27}$,
P(Y=2)=${C}_{3}^{2}(\frac{2}{3})^{2}(\frac{1}{3})$=$\frac{12}{27}$,
P(Y=3)=${C}_{3}^{3}(\frac{2}{3})^{3}$=$\frac{8}{27}$,
∴Y的分布列是:
| Y | 0 | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{6}{27}$ | $\frac{12}{27}$ | $\frac{8}{27}$ |
(Ⅲ)DX=(1-2)2×$\frac{1}{5}$+(2-2)2×$\frac{3}{5}$+(3-2)2×$\frac{1}{5}$=$\frac{2}{5}$,
∵Y∽B(3,$\frac{2}{3}$),∴DY=3×$\frac{2}{3}×\frac{1}{3}$=$\frac{2}{3}$
∴DX<DY,
∵P(X≥2)=$\frac{3}{5}+\frac{1}{5}=0.8$,P(Y≥2)=$\frac{12}{27}+\frac{8}{27}$≈0.74
∴P(X≥2)>P(Y≥2)
①从做对题数的数学期望考查,两人水平相当;从做对题数的方差考查,甲较稳定;
②从至少完成2题的概率考查,甲获得通过的可能性大,
因此,可以判断甲的实验操作能力强.
点评 本题考查随机变量的分布列和数学期望,考查概率知识 的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.点M,N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,则MN和CD1所成角的大小为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
11.直线x=a分别与曲线y=2(x+1),y=x+lnx交于A、B两点,则|AB|的最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{3}{2}$ |
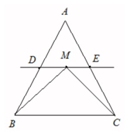 在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.
在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.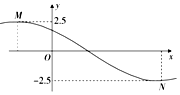 已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )
已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )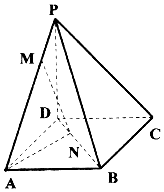 如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.