Question

在半径为1的圆上随机地取两点，连成一条弦，则其长超过圆内接等边三角形的边长的概率是多少？

Answer 1

分析：在圆上随机取两点，可以看成先取定一点后，再随机地取另一点，如图所示，可取定B点，当另一点E取在劣弧CD上时，|BE|＞|BC|.

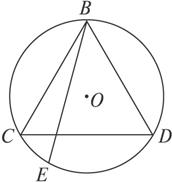
解：记事件A={弦长超过圆内接等边三角形的边长}，取圆内接等边△BCD的顶点B为弦的一个端点，当另一点在劣弧CD上时，|BE|＞|BC|，而劣弧CD的弧长是圆周长的，所以由几何概率公式得P(A)=.

即弦长超过圆内接等边三角形的边长的概率是.