题目内容
称满足以下两个条件的有穷数列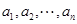 为
为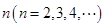 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若数列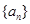 的通项公式是
的通项公式是 ,
,
试判断数列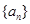 是否为2014阶“期待数列”,并说明理由;
是否为2014阶“期待数列”,并说明理由;
(2)若等比数列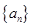 为
为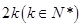 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及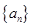 的通项公式;
的通项公式;
(3)若一个等差数列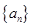 既是
既是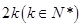 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
【答案】
(1)是;
(2) .
. 或
或 ;
;
(3) ;
;
【解析】
试题分析:(1)判断数列 是不是为2014阶“期待数列”,就是根据定义计算
是不是为2014阶“期待数列”,就是根据定义计算 ,
, ,是不是一个为0,一个为1,如是则是“期待数列”,否则就不是;(2)数列
,是不是一个为0,一个为1,如是则是“期待数列”,否则就不是;(2)数列 中等比数列,因此
中等比数列,因此 是其前
是其前 和,故利用前前
和,故利用前前 项和公式,分
项和公式,分 和
和 进行讨论,可很快求出
进行讨论,可很快求出 ,
, 或
或 ;(3)
;(3) 阶等差数列是递增数列,即公差
阶等差数列是递增数列,即公差 ,其和为0,故易知数列前面的项为负,后面的项为正,即前
,其和为0,故易知数列前面的项为负,后面的项为正,即前 项为正,后
项为正,后 项为正,因此有
项为正,因此有 ,
, ,这两式用基本量或直接相减可求得
,这两式用基本量或直接相减可求得 ,
, ,因此通项公式可得.
,因此通项公式可得.
试题解析:(1)因为 ,
2分
,
2分
所以

 ,
,
所以数列 为2014阶“期待数列”
4分
为2014阶“期待数列”
4分
(2)①若 ,由①得,
,由①得, ,得
,得 ,矛盾. 5分
,矛盾. 5分
若 ,则由①
,则由①
 =0,得
=0,得 , 7分
, 7分
由②得 或
或 .
.
所以, .数列
.数列 的通项公式是
的通项公式是
或 9分
9分
(3)设等差数列 的公差为
的公差为 ,
, >0.
>0.
∵ ,∴
,∴ ,∴
,∴ ,
,
∵ >0,由
>0,由 得
得 ,
, ,
11分
,
11分
由①、②得 ,
, , 13分
, 13分
两式相减得, , ∴
, ∴ ,
,
又 ,得
,得 ,
,
∴数列 的通项公式是
的通项公式是 . 16分
. 16分
考点:(1)三角函数的诱导公式与新定义的理解;(2)等比数列的前 和公式与通项公式;(3)等差数列的前
和公式与通项公式;(3)等差数列的前 和公式与通项公式.
和公式与通项公式.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
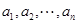 为
为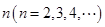 阶“期待数列”:
阶“期待数列”: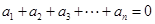 ;②
;②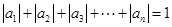 .
. 为
为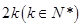 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的前k项和为
的前k项和为 :
: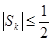 ;
;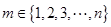 使
使 ,试问数列
,试问数列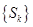 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.