题目内容
18．一个等比数列前n项和为Sn=48，前2n项之和S2n=60，求S3n．分析 由等比数列的性质可得Sn，S2n-Sn，S3n-S2n成等比数列，代入已知数据计算可得．
解答 解：由等比数列的性质可得Sn，S2n-Sn，S3n-S2n成等比数列，
∴48，12，S3n-60成等比数列，
∴48（S3n-60）=122，
解得S3n=63
点评 本题考查等比数列的求和公式的性质，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．如图$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的两个单位向量，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=（ ）
| A． | $4\sqrt{2}$ | B． | $2\sqrt{10}$ | C． | $2\sqrt{13}$ | D． | $2\sqrt{15}$ |
6．定义域为D的单调函数y=f（x），如果存在区间[m，n]⊆D，满足当定义域为是[m，n]时，f（x）的值域也是[m，n]，则称[m，n]是该函数的“可协调区间”；如果函数y=$\frac{（{a}^{2}+a）x-1}{{a}^{2}x}$（a≠0）的一个可协调区间是[m，n]，则实数a的取值范围是（ ）
| A． | -3＜a＜1 | B． | -3＜a＜0 | C． | 0＜a＜1 | D． | a＜-3或a＞1 |
5．抛物线x2=y的准线方程是（ ）
| A． | x=$\frac{1}{2}$ | B． | y=$\frac{1}{2}$ | C． | x=-$\frac{1}{4}$ | D． | $y=-\frac{1}{4}$ |
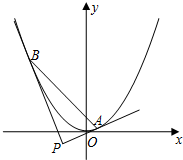已知抛物线x2=2py（p＞0）的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合．