题目内容
12．抛物线y=-$\frac{1}{8}$x2的准线方程是y=2．分析 由x2=-2py的准线方程为y=$\frac{p}{2}$，抛物线y=-$\frac{1}{8}$x2即为x2=-8y的准线方程即可求得．
解答 解：由x2=-2py的准线方程为y=$\frac{p}{2}$，
抛物线y=-$\frac{1}{8}$x2即为x2=-8y的准线方程为y=2．
故答案为：y=2．
点评 本题考查抛物线的方程和性质，主要考查抛物线的准线方程的求法，属于基础题．
练习册系列答案
相关题目
20．一个几何体的三视图如图所示，图中直角三角形的直角边长均为1，则该几何体体积为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{{\sqrt{2}}}{6}$ | C． | $\frac{{\sqrt{3}}}{6}$ | D． | $\frac{1}{2}$ |
7．
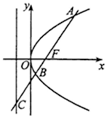如图，过抛物线y2=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（ ）
如图，过抛物线y2=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（ ）| A． | y2=3x | B． | y2=9x | C． | y2=$\frac{3}{2}$x | D． | y2=$\frac{9}{2}$x |