题目内容
下列四个命题,其中为真命题的是( )
A.命题“若 ,则 ,则 或 或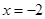 ”的逆否命题是“若 ”的逆否命题是“若 或 或 ,则 ,则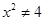 ” ” |
B.若命题 所有幂函数的图像不过第四象限,命题 所有幂函数的图像不过第四象限,命题 所有抛物线的离心率为 所有抛物线的离心率为 ,则命题“ ,则命题“ 且 且 ”为真 ”为真 |
C.若命题  则 则 |
D.若 ,则 ,则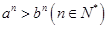 |
B
解析试题分析: :命题“若
:命题“若 ,则
,则 或
或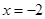 ”的逆否命题是“若
”的逆否命题是“若 且
且 ,则
,则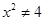 ”;
”; :
: 所以命题
所以命题 为真,由抛物线的定义命题
为真,由抛物线的定义命题 为真
为真 “
“  且
且 ” 为真;
” 为真; :
: ;
; :
: .
.
考点:命题与量词,基本逻辑联结词,幂函数,不等式的性质.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知数列 ,那么“对任意的
,那么“对任意的 ,点
,点 都在直线
都在直线 上”是“
上”是“ 为等差数列”的 ( )
为等差数列”的 ( )
| A.必要而不充分条件 | B.既不充分也不必要条件 |
| C.充要条件 | D.充分而不必要条件 |
已知“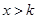 ”是“
”是“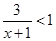 ”的充分不必要条件,则k的取值范围是( )
”的充分不必要条件,则k的取值范围是( )
A.[2,+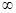 ) ) | B.[1,+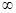 ) ) | C.(2,+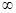 ) ) | D.(一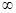 ,-1] ,-1] |
给出下列四个结论:
①若命题 ,则
,则 ;
;
② “ ”是“
”是“ ”的充分而不必要条件;
”的充分而不必要条件;
③命题“若 ,则方程
,则方程 有实数根”的逆否命题为:“若方程
有实数根”的逆否命题为:“若方程 没有实数根,则
没有实数根,则 0”;
0”;
④若 ,则
,则 的最小值为
的最小值为 .
.
其中正确结论的个数为 ( )
A. | B. | C. | D. |
用反证法证明命题:若整数系数的一元二次方程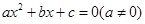 有有理实数根,那么
有有理实数根,那么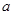 ,
,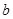 ,
,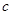 中至少有一个是偶数,下列假设中正确的是( )
中至少有一个是偶数,下列假设中正确的是( )
A.假设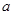 , ,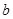 , ,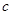 至多有一个是偶数 至多有一个是偶数 |
B.假设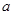 , ,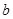 , ,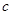 至多有两个偶数 至多有两个偶数 |
C.假设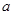 , ,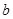 , ,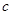 都是偶数 都是偶数 |
D.假设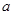 , ,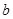 , ,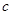 都不是偶数 都不是偶数 |
下列说法正确的是( )
A.“ ”是“ ”是“ 在 在 上为增函数”的充要条件 上为增函数”的充要条件 |
B.命题“ 使得 使得 ”的否定是:“ ”的否定是:“ ” ” |
C.“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
D.命题p:“ ”,则 ”,则 p是真命题 p是真命题 |
若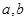 都是实数,则“
都是实数,则“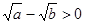 ”是“
”是“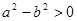 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“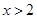 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |