题目内容
若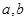 都是实数,则“
都是实数,则“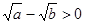 ”是“
”是“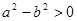 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:由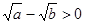 得
得 ,由
,由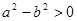 得
得 ,即
,即 或
或 ,所以“
,所以“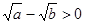 ”是“
”是“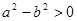 ”的充分而不必要条件.
”的充分而不必要条件.
考点:1.充要条件;2.不等式的性质.

练习册系列答案
相关题目
“a≥0”是“函数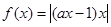 在区间(-∞,0)内单调递减”的( )
在区间(-∞,0)内单调递减”的( )
| A.充要条件 | B.必要不充分条件 |
C.充分不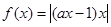 必要条件 必要条件 | D.即不充分也不必要条件 |
下列四个命题,其中为真命题的是( )
A.命题“若 ,则 ,则 或 或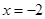 ”的逆否命题是“若 ”的逆否命题是“若 或 或 ,则 ,则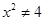 ” ” |
B.若命题 所有幂函数的图像不过第四象限,命题 所有幂函数的图像不过第四象限,命题 所有抛物线的离心率为 所有抛物线的离心率为 ,则命题“ ,则命题“ 且 且 ”为真 ”为真 |
C.若命题  则 则 |
D.若 ,则 ,则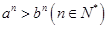 |
已知q是等比数列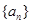 的公比,则“
的公比,则“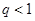 ”是“数列
”是“数列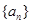 是递减数列”的( )
是递减数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列说法错误的是( )
A.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
B.命题“若 ,则 ,则 ”的否命题是:“若 ”的否命题是:“若 ,则 ,则 ” ” |
C.若命题 ,则 ,则  |
D.若命题“ ”与命题“ ”与命题“ 或 或 ”都是真命题,那么命题 ”都是真命题,那么命题 一定是真命题 一定是真命题 |
若命题“ R,使得x02+mx0+2m-3<0”为假命题,则实数m的取值范围是( )
R,使得x02+mx0+2m-3<0”为假命题,则实数m的取值范围是( )
| A.[2,6] | B.[-6,-2] | C.(2,6) | D.(-6,-2) |
下列说法错误的是( )
A.命题“若 ,则 ,则 ”的逆否命题为:“若 ”的逆否命题为:“若 ,则 ,则 ” ” |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.若 且 且 为假命题,则 为假命题,则 、 、 均为假命题 均为假命题 |
D.命题 :“ :“ ,使得 ,使得 ”,则 ”,则 :“ :“ ,均有 ,均有 ” ” |
设 ,则“
,则“ ”是“复数
”是“复数 为纯虚数”的( )
为纯虚数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
 ,并设:
,并设:
 ,
, 至少有3个实根;
至少有3个实根; 当
当 时,方程
时,方程 当
当 时,方程
时,方程


