Question

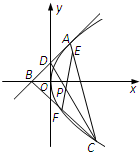过抛物线y²=4x上一点A（1，2）作抛物线的切线，分别交x轴于点B，交y轴于点D，点C（异于点A）在抛物线上，点E在线段AC上，满足

AE

=λ₁

EC

；点F在线段BC上，满足

BF

=λ₂

FC

，且λ₁+λ₂=1，线段CD与EF交于点P．
（1）设

DP

=λ

PC

，求λ；
（2）当点C在抛物线上移动时，求点P的轨迹方程．

Answer 1

分析：（1）设出过A点的切线方程，确定出D点，分别表示出

DP

，

PC

，根据λ₁+λ₂=1，求出λ的值．
（2）设C（x₀，y₀），P（x，y），用x₀，y₀表示出x，y，代入抛物线方程，进而确定P点的轨迹．

解答：解：（1）过点A的切线方程为y=x+1． …（1分）
切线交x轴于点B（-1，0），交y轴交于点D（0，1），则D是AB的中点．
所以

CD

=

1

2

(

CA

+

CB

)．                            （1）…（3分）
由

DP

=λ

PC

⇒

DP

+

PC

=（1+λ）

PC

⇒

CD

=(1+λ)

CP

． （2）
同理由 

AE

=λ₁

EC

，得

CA

=（1+λ₁）

CE

，（3）

BF

=λ₂

FC

，得

CB

=（1+λ₂）

CF

．     （4）
将（2）、（3）、（4）式代入（1）得

CP

=

1

2(1+λ)

[(1+λ1)

CE

+(1+λ2)

CF

]．
因为E、P、F三点共线，所以 

1+λ1

2(1+λ)

+

1+λ2

2(1+λ)

=1，
再由λ₁+λ₂=1，解之得λ=

1

2

．…（6分）
（2）由（1）得CP=2PD，D是AB的中点，所以点P为△ABC的重心．
所以，x=

1-1+x0

3

，y=

2+0+y0

3

．
解得x₀=3x，y₀=3y-2，代入y₀²=4x₀得，（3y-2）²=12x．
由于x₀≠1，故x≠

1

3

．所求轨迹方程为（3y-2）²=12x （x≠

1

3

）． …（10分）

点评：本题以抛物线为载体，考查曲线的轨迹方程的探求及综合应用能力．