题目内容
在△ABC中,若sinA+sinB=sinC•(cosA+cosB),试判断△ABC的形状.
解:∵sinB=sin[180°-(A+C)]=sin(A+C)=sinAcosC+cosAsinC,
又∵sinA+sinB=sinC•(cosA+cosB),
∴sinA+sinAcosC+cosAsinC=sinCcosA+sinCcosB,
∴sinA=sinCcosB,
∴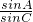 =cosB,
=cosB,
∵ =
= ,
,
∴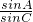 =
= ,
,
又∵cosB= ,
,
∴ =
= ,
,
∴2a2=a2+c2-b2,
∴a2+b2=c2,
∴△ABC是直角三角形.
分析:利用三角形中,sinB=sin(A+C)可求得sinB=sinAcosC+cosAsinC,与已知sinA+sinB=sinC•(cosA+cosB)联立,可求得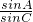 =cosB,再利用正弦定理与余弦定理转化为边之间的关系,可判断△ABC的形状.
=cosB,再利用正弦定理与余弦定理转化为边之间的关系,可判断△ABC的形状.
点评:本题考查三角形的形状判断,着重考查正弦定理与余弦定理,求得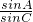 =cosB是转化的关键,属于中档题.
=cosB是转化的关键,属于中档题.
又∵sinA+sinB=sinC•(cosA+cosB),
∴sinA+sinAcosC+cosAsinC=sinCcosA+sinCcosB,
∴sinA=sinCcosB,
∴
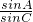 =cosB,
=cosB,∵
 =
= ,
,∴
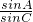 =
= ,
,又∵cosB=
 ,
,∴
 =
= ,
,∴2a2=a2+c2-b2,
∴a2+b2=c2,
∴△ABC是直角三角形.
分析:利用三角形中,sinB=sin(A+C)可求得sinB=sinAcosC+cosAsinC,与已知sinA+sinB=sinC•(cosA+cosB)联立,可求得
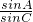 =cosB,再利用正弦定理与余弦定理转化为边之间的关系,可判断△ABC的形状.
=cosB,再利用正弦定理与余弦定理转化为边之间的关系,可判断△ABC的形状.点评:本题考查三角形的形状判断,着重考查正弦定理与余弦定理,求得
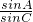 =cosB是转化的关键,属于中档题.
=cosB是转化的关键,属于中档题. 
练习册系列答案
相关题目
在△ABC中,若sinA:sinB:sinC=5:7:8,则此三角形的最大角与最小角之和为( )
| A、90° | B、120° | C、135° | D、150° |