题目内容
已知函数 .
.
(1)若对于区间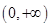 内的任意
内的任意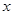 ,总有
,总有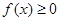 成立,求实数
成立,求实数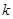 的取值范围;
的取值范围;
(2)若函数 在区间
在区间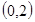 内有两个不同的零点
内有两个不同的零点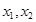 ,求:
,求:
①实数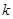 的取值范围; ②
的取值范围; ②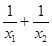 的取值范围.
的取值范围.
(1)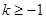 ;(2)
;(2)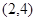 .
.
解析试题分析:(1)分离参数,若对于区间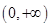 内的任意
内的任意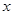 ,总有
,总有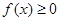 成立,得
成立,得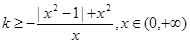 ,再求出
,再求出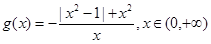 的最大值即可;
的最大值即可;
(2)先去绝对值,当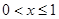 时,方程
时,方程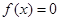 化为
化为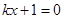 ,
,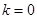 时,无解;
时,无解;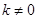 时,
时,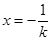 ;
;
当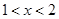 时,方程
时,方程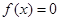 化为
化为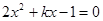 ,
,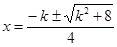 ,而其中
,而其中 ,故
,故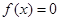 在区间
在区间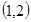 内至多有一解
内至多有一解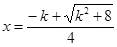 ;
;
综合ⅰ)ⅱ)可知,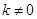 ,且
,且 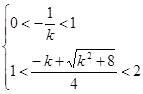 ,得
,得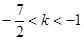 .
.
试题解析:(1)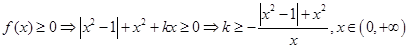 ,
,
记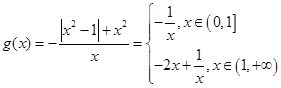 ,易知
,易知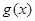 在上
在上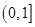 递增,在
递增,在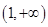 上递减,
上递减,
∴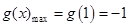 ,∴
,∴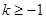 即可 (5分)
即可 (5分)
(2)①ⅰ)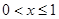 时,方程
时,方程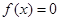 化为
化为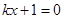 ,
,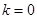 时,无解;
时,无解;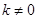 时,
时,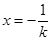 ;
;
ⅱ)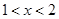 时,方程
时,方程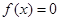 化为
化为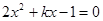 ,
,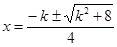 ,而其中
,而其中 ,故
,故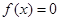 在区间
在区间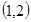 内至多有一解
内至多有一解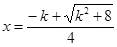 ;
;
综合ⅰ)ⅱ)可知,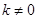 ,且
,且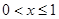 时,方程
时,方程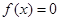 有一解
有一解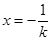 ,故
,故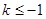 ;
;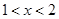 时,方程
时,方程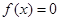 也仅有一解
也仅有一解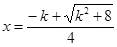 ,令
,令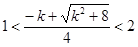 ,得
,得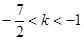 ,所以实数
,所以实数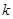 的取值范围是
的取值范围是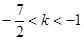 ; (10分)
; (10分)
②方程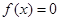 的两解分别为
的两解分别为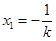 ,
,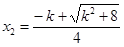 ,
,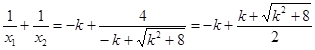
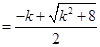
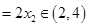 (14分)
(14分)
考点:(1)绝对值,不等式的恒成立问题;(2)函数与方程,函数的零点

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
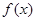 定义在
定义在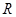 上,对任意的
上,对任意的 ,
,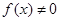 ,且
,且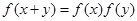 .
.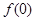 ,并证明:
,并证明: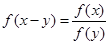 ;
;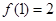 .设向量
.设向量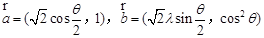 ,对任意
,对任意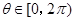 ,
, 恒成立,求实数
恒成立,求实数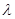 的取值范围.
的取值范围.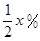 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大? 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足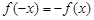 ,则称
,则称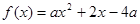
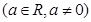 ,试判断
,试判断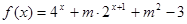 为定义域
为定义域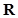 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围.
 时,该商品的价格上涨多少,才能使销售的总金额达到最大?
时,该商品的价格上涨多少,才能使销售的总金额达到最大?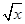 )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.