题目内容
【题目】已知直线l:![]() 与拋物线C:
与拋物线C:![]() 相切.
相切.
(1)求拋物线方程;
(2)斜率不为0的直线![]() 经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线
经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线![]() 对称.若存在求出斜率k的取值范围;若不存在,说明理由.
对称.若存在求出斜率k的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析
;(2)不存在,理由见解析
【解析】
(1)联立直线的方程和抛物线方程,利用判别式为零列方程,解方程求得![]() ,由此求得抛物线方程.
,由此求得抛物线方程.
(2)设出直线![]() 的方程,根据对称性设出直线
的方程,根据对称性设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和抛物线方程,化简后写出根与系数关系以及判别式,由此求得
的方程和抛物线方程,化简后写出根与系数关系以及判别式,由此求得![]() 中点
中点![]() 的坐标,将
的坐标,将![]() 点坐标代入直线
点坐标代入直线![]() 的方程,化简后判断出符合题意的
的方程,化简后判断出符合题意的![]() 不存在.
不存在.
![]() 由题联立方程组
由题联立方程组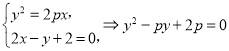 .
.
因为直线l与拋物C相切,所以![]() ,
,![]() 舍
舍![]() ,
,
所以抛物线C的方程为![]() .
.
![]() 由
由![]() 可知
可知![]() ,所以可设直线
,所以可设直线![]() 的方程为
的方程为![]() .
.
假设抛物线C上存在两点D,E关于直线![]() 对称,
对称,
可设直线DE的方程为![]() ,
,
联立方程组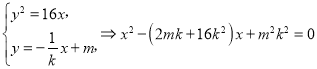 .
.
由![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,DE中点为
,DE中点为![]() ,
,
则![]() ,
,![]() ,
,
因为![]() 在直线
在直线![]() 上,所以将其代入方程
上,所以将其代入方程![]() ,
,
得![]() ,即
,即![]() ,
,
代入![]() ,得
,得![]() ,
,
所以k无解,故不存在.
即抛物线C上不存在两点D,E关于过焦点的直线![]() 对称.
对称.

练习册系列答案
相关题目